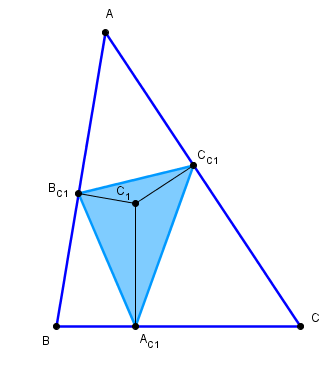
Triangle inscrit - solution

Etant donné un triangle ABC (quelconque, mais pourquoi pas de côtés 3,4,5 pour fixer les idées), construire le plus petit triangle semblable inscrit dans ABC, un sommet sur chaque côté.

Considérons un triangle A"B"C" semblable 'circonscrit' à ABC, c'est à dire dont les côtés contiennent les sommets A,B,C.
Alors la figure formée par A"B"C" et son triangle inscrit ABC est semblable à la figure cherchée ABC et son triangle inscrit A'B'C'.
Le problème revient donc à chercher le plus grand triangle A"B"C" circonscrit.
Il y a 6 cas à étudier, selon les permutations de A,B,C.
Considérons le cas où A est sur B"C" (donc A' sur BC), B sur A"B" et C sur A"C".
Alors A" est sur l'arc de cercle d'où on voit BC sous l'angle A.
De même pour B" sur l'arc d'où on voit AB sous l'angle B, et C" sur l'arc d'où on voit AC sous l'angle C.
Si on choisit librement A" sur son arc, B" et C" s'en déduisent. Reste donc à trouver A" pour que A"B" soit maximum.
Soient Oa et Ob les centres des arcs capables, I et J les projections de Oa et Ob sur A"B".
Bien évidemment A"B" = 2 IJ. La projection de OaOb sera maximum quand A"B" // OaOb.
La construction de A"B"C" maximum est alors immédiate, et A'B'C' s'en déduit par similitude.
La solution n'est valable que si chaque sommet de ABC est sur les côtés mêmes, et non leur prolongements.
Sinon, le plus grand A"B"C" est limité avec A,B ou C dans un angle.

Les centres des arcs capables sont construits ainsi :
Si l'angle est adjacent au côté, c'est l'intersection de la médiatrice et de la perpendiculaire à l'autre côté
(par exemple ici, l'arc capable de B" est tangent en B à BC, donc BOb _|_ BC).
Si l'angle est opposé, c'est le symétrique du centre O du cercle circonscrit par rapport au côté (par exemple ici Oa).
L'arc capable est alors le symétrique du cercle circonscrit.

Les 6 cas pour un triangle quelconque :

Sommets A'B'C' sur les cotés de ABC				Arcs capables
	AB	BC	AC		AB	BC	AC
1	A'	C'	B'		A	C	B
2	B'	C'	A'		A	B	C
3	A'	B'	C'		B	C	A
4	B'	A'	C'		B	A	C
5	C'	B'	A'		C	B	A
6	C'	A'	B'		C	A	B

Le point C est contraint à AB ≥ BC ≥ AC (tout disparaît sinon) dans la zone délimitée en jaune par la médiatrice de AB (BC ≥ AC) et l'arc de cercle de centre B (AB ≥ BC).
Les dimensions de A'B'C' sont affichées en rouge si le triangle est "bloqué" dans un angle.

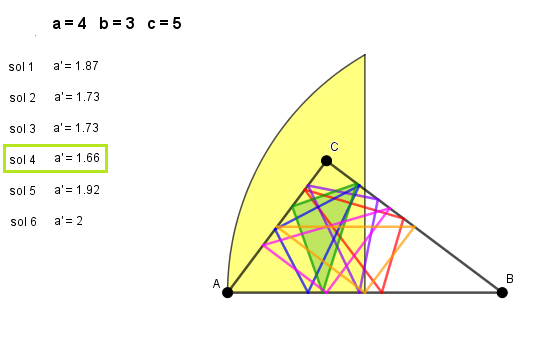
On "voit" que pour le triangle de départ (AB=5, BC=4, AC=3) le plus petit A'B'C' est le cas 4 (A' sur BC, B' sur AB et C' sur AC).
De façon générale, il semble naturel que pour le plus petit A'B'C', le plus grand côté de A'B'C' soit dans le plus petit angle de ABC et le plus petit côté de A'B'C' dans le plus grand angle de ABC.

Calcul des côtés

Dans ce cas donc, plus petit triangle semblable dans un triangle de côtés (3,4,5) :
Le point H milieu de AB donne BH = 5/2.
Le triangle BOH semblable à ABC donne BO/AB = BH/AC, soit OB = 5×(5/2)/3 = 25/6
OM² = 4² + (25/6 - 3/2)² = 208/9 et OM = 4√13/3
Alors B"C" = 2 OM = 8√13/3
Le triangle inscrit A'B'C' est à ABC ce que ABC est à A"B"C" et donc B'C'/BC = BC/B"C", soit :

 B'C' = 4² × 3/(8√13) = 6/√13 ≈ 1.664... 

Les deux autres côtés sont alors immédiatement  3B'C'/4 ≈ 1.248... et 5B'C'/4 ≈ 2.080... 

Le calcul dans les 5 autres cas n'est pas bien plus compliqué, mais fastidieux.

Advanced Euclidean Geometry ...

Rappelons que tous les triangles inscrits de même forme et "de la même façon" ont un centre de similitude commun (point de Miquel)
Le plus petit est donc le triangle podaire de ce point de Miquel.
On est donc amené à chercher les points dont le triangle podaire est semblable au triangle de départ
Il y en a 11 :

• Le centre du cercle circonscrit (qui donne le triangle médian, directement semblable de rapport 1/2
• Le "1er" point de Brocard donnant un triangle directement semblable
• Le "1me" point de Brocard donnant un triangle directement semblable aussi
• les trois sommets du "second" triangle de Brocard, donnant des triangles inversement semblables
• et enfin les inverse de ces points par rapport au cercle circonscrit
  sauf de O bien entendu, ce qui donne 5 autres triangles mais jamais à l'intérieur, donc sans intérêt ici

Même certains des 6 "normaux" ne tombent pas toujours à l'intérieur (voir ci dessus)
Il faudrait alors "tourner" ces triangles autour de leur centre de similitude pour faire coïncider le sommet "qui dépasse" avec le sommet du triangle d'origine.

donnons (ou rappelons) des constructions de tous ces points

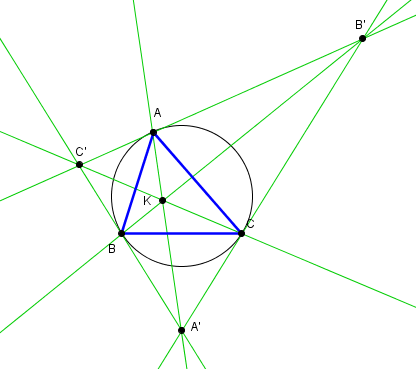
Point de Lemoine K

C'est le conjugué isogonal du centre de gravité, point de concours des symédianes.
On trace le triangle tangentiel A'B'C' formé des tangentes au cercle circonscrit en les sommets du triangle
Les symédianes sont les droites AA', BB' et CC'

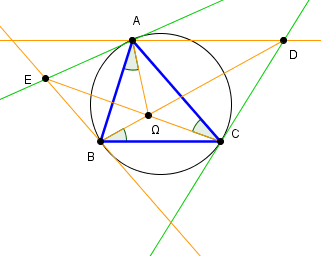
Points de Brocard

Définis comme formant des angles égaux avec les cotés.
Une construction simple à partir des tangentes précédentes :
la tangente en C et la parallèle à (BC) par A se coupent en D
la tangente en A et la parallèle à (CA) par B se coupent en E
(la tangente en B et la parallèle à (AB) par C se coupent en F)
les droites BD, CE (et AF) sont concourantes en Ω premier point de Brocard

Le second point de Brocard se construit de la même façon mais en "tournant" dans l'autre sens

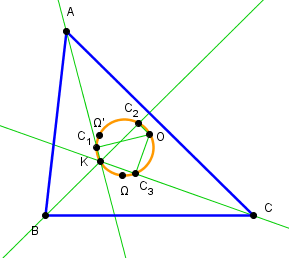
Second triangle de Brocard

Il est construit comme projections orthogonales du centre du cercle circonscrit sur les symédianes

On notera que tous ces points sont situés sur le "cercle de Brocard" de diamètre OK