3 cercles

Etant donné un triangle ABC quelconque, inscrire trois cercles égaux dans ce triangle, chaque côté du triangle tangent à au moins un des trois cercles.

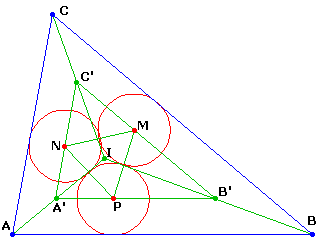
Appelons M,N,P les centres des cercles cherchés. MNP est évidemment un triangle équilatéral.
Soit I le centre du cercle inscrit dans ABC.
Considérons le triangle A'B'C' formé par les parallèles à ABC passant par M,N,P.
Ce triangle est homothétique de ABC dans une homothétie de centre I.
(Car les distances entre les côtés de ABC et de A'B'C' sont égales, le cercle inscrit de ABC et celui de A'B'C' ont donc même centre I)
Le triangle MNP est alors un triangle équilatéral inscrit dans A'B'C'.

Cette remarque permet de construire facilement trois cercles répondant à la question.
La construction la plus simple est avec une orientation (directions des côtés de MNP) donnée.
Inscrire dans ABC un triangle équilatéral M'N'P' d'orientation donnée. Soit 2s son côté.
Cette construction est élémentaire par homothétie de centre C, sur un triangle équilatéral quelconque M"N"P", M"N" parallèle à la direction donné.

Soit alors T' le point à distance s perpendiculairement à BC, extérieur à ABC.
T' est le point de contact d'un cercle de centre M' et de rayon s avec un triangle A"B"C" homothétique à ABC
Les cercles de centre M',N',P' et de rayon s formant une solution pour le triangle A"B"C"

On transforme alors cette solution par l'homothétie A"B"C" → ABC :
Cette homothétie a pour centre I, centre du cercle inscrit à ABC (comme ci-dessus).
IT' coupe BC en le point de contact T avec BC du cercle cherché.
Son centre M est l'homothétique de M', de centre I et de rapport IT/IT'
N et P sont homothétiques de N' et P' dans la même homothétie.

On voit ainsi qu'il y a une infinité de solutions, selon la direction choisie de MN.
Dans l'applet, A, B, C sont bien entendu déplaçables. Les points M" et N" déplaçables définissent la direction de MN.
Certaines orientations de MN sont impossibles : le triangle équilatéral inscrit "déborde" de ABC, ses sommets étant sur les droites indéfinies AB, BC, AC et non sur les côtés même. Dans ces conditions, les cercles "débordent" aussi...

Reste alors à trouver le plus petit rayon possible pour ces cercles.
Les cercles inscrits dans A"B"C" ont pour rayon s
L'homothétie de centre I transformant A"B"C" en ABC a pour rapport r/(r + s), r étant le rayon du cercle inscrit de ABC.
Les cercles inscrits dans ABC ont donc pour rayon ρ = s.r/(r + s)
Cette fonction strictement croissante de s pour s > 0 montre que ρ est minimum quand s est minimum (resp. maximum quand s maximum). Et donc

Le rayon ρ des cercles inscrits dans ABC est minimum quand le triangle M'N'P' est minimum

Il suffit donc de chercher le plus petit triangle équilatéral M'N'P' inscrit dans ABC.
Rappelons que le plus petit triangle équilatéral inscrit est parallèle au "triangle de Napoléon" défini par les centres des triangles équilatéraux construits sur les côtés de ABC.
La construction des plus petits cercles égaux inscrits dans ABC peut alors être :
Construire les centres U et V des triangles équilatéraux sur AC et BC,
Intersection des angles BCU et CBU à 30°, et de même sur AC avec ACV = CAV = 30°.
Le triangle M'N'P' correspondant avec M'N' // UV est alors construit comme précédemment, puis MNP par homothétie de centre I.

Quant au plus grand rayon, l'étude des triangles équilatéraux inscrits montre qu'il s'agit de cas "dégénérés" où l'un au moins des côtés du triangle équilatéral M'N'P' est sur un des côtés de ABC, avec un sommet du triangle équilatéral en A, B ou C.
Ce sommet du triangle équilatéral est donc dans un angle de ABC ≥ 60°
Il y a bien entendu dans tout triangle au moins un angle ≥ 60°, et au moins un angle ≤ 60°
Sans perte de généralité, appelons A l'angle ≥ 60° et C l'angle ≤60°.
Il y a alors à priori 3 possibilités de placer un triangle équilatéral maximal dans l'angle A. Un côté sur AB, un côté sur AC ou un côté sur BC.
Ici les conditions du problème n'interdisent pas au triangle M'N'P' d'avoir un sommet et un côté opposé communs avec ABC :
Ceci donne un cercle tangent à AB et AC et les deux autres tangents à BC, "chaque côté est tangent à au moins un cercle".

La solution avec le côté sur AC est toujours possible (puisque l'angle C est ≤ 60°)
La solution avec le côté sur AB n'est possible que si l'angle B est aussi ≤60°
Dans ces conditions (B ≤60°), soit AH la hauteur issue de A. L'angle BAH est alors supérieur à 30° et une solution avec le côté sur BC est aussi possible, et est de façon évidente plus grande que les deux autres.

Il reste à examiner le dernier cas où A et B sont tous deux ≥ 60°
Dans ce cas, il y a deux et seulement deux possibilités à envisager (car BAH < 30°) :
Angle en A, côté sur AC, et angle en B, côté sur BC

L'applet impose A dans le domaine C<60°, A>B et A>60°
Les seuls candidats sont alors dans l'angle A seul (3 candidats) si B <60° ou dans l'angle A et l'angle B (2 candidats) si B > 60°

L'angle AM'B = C + π/3 donne alors, en appelant c le côté AB et 2s le côté du triangle équilatéral :
c / sin(C + π/3) = 2s / sin(B) soit s = (c/2).sin(B) / sin(C + π/3) = K.sin(B)
Le côté du triangle équilatéral dans l'angle B est de même s' = (c/2).sin(A) / sin(C + π/3) = K.sin(A) avec la même valeur de K.
(s' - s)/K = sin(A) - sin(B) = 2 cos((A + B)/2) sin((A - B)/2)
Comme A + B < π soit (A + B)/2 < π/2 et cos((A + B)/2) > 0, s' - s est du signe de A - B
Par conséquent

Le triangle équilatéral maximal est dans le plus petit angle ≥ 60°   Si c'est le seul angle ≥ 60°, le côté opposé est sur le côté opposé   Sinon, le coté est adjacent, en direction de l'angle <60°