Ellipses de Steiner

Etant donné un triangle ABC quelconque, il existe deux ellipses, dites de Steiner :
L'une tangente aux 3 cotés en leurs milieux
L'autre passant par les 3 sommets, les tangentes en ces points étant parallèles au côté opposé.

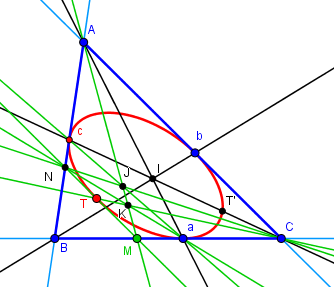Une première remarque est que si on choisit 2 points quelconques a et b sur les côtés BC et AC, il existe une conique tangente en a à BC, tangente en b à AC et tangente en un point c à AB.
Le théorème de Brianchon permet de construire c facilement : abc est un triangle Cévien, c'est à dire que Aa Bb et Cc sont concourantes, en considérant l'hexagone AbCaBc.
Si ceci suffit théoriquement pour tracer la conique (on a même 6 points), dans la pratique on obtient des points d'intersection à l'infini, puisque dans le cas qui nous occupe (a,b,c milieux des segments) ab parallèle à AB, ou alors des points confondus.
On obtient toutefois aisément, avec Brianchon, une nouvelle tangente et son point de contact :
Une tangente "courante" s'obtient en choisissant un point M quelconque de BC, et en construisant le point correspondant N sur AB : ac et AM se coupent en J, CJ coupe AB en N. (hexagone ACaMNc)
Le point de contact de cette tangente est obtenu comme à la première étape : les droites AM, Na et CT sont concourantes. (hexagone ACaMTN)
On ainsi suffisamment de points distincts pour tracer la conique, par exemple à partir des points c,c,b,a,T (la droite cc étant la tangente AB).

Ici ce qui est remarquable est que si a et b sont les milieux de BC et AC, alors c est aussi le milieu de AB. Une première preuve est issue directement de la construction précédente : les céviennes sont les médianes.
Mais on peut aussi conclure "immédiatement" par une transformation affine du triangle ABC en un triangle équilatéral, l'image de l'ellipse étant alors le cercle inscrit.
La transformation affine conserve les alignements, les rapports de segments alignés (milieux) et les tangences. Elle transforme une conique en une autre conique de même "genre", ici le cercle en une ellipse.
On déduit immédiatement (alignements sur les médianes) que le centre de cette ellipse est le centre de gravité du triangle.
Une simple homothétie de centre G et de rapport -2 transforme cette ellipse en une ellipse tangente en A,B,C, milieux des côtés du triangle dont ABC est le triangle médian. Les tangentes en A,B,C sont donc parallèles aux côtés de ABC.

Triangle 1/7

Les "trimédianes", coupant le côté opposé au 1/3, définissent deux triangles abc et a'b'c' dont l'aire est 1/7 ABC.
La propriété qui nous intéresse ici est

 a,b,c,a',b',c' sont sur une même ellipse 

Et qui plus est : cette ellipse est homothétique des ellipses de Steiner.
Le centre de l'homothétie étant G comme de bien entendu.

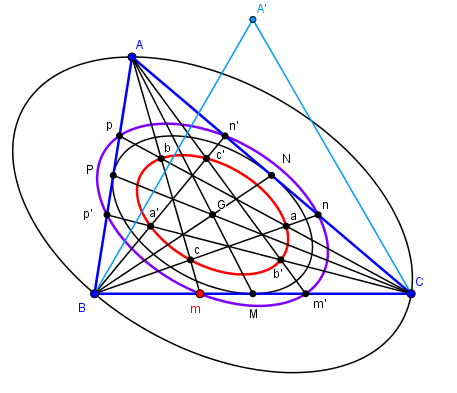
A,B,C et m sont déplaçables, m définit le rapport Bm/BC
La propriété est évidente pour un triangle équilatéral : les 6 points sont cocycliques, et le centre du cercle est G.
Le rayon de ce cercle r s'obtient immédiatement car la transformation affine conserve le rapport des aires :
Dans le triangle équilatéral, notre triangle abc a pour aire 1/7 de l'aire de ABC.
Un triangle équilatéral inscrit dans le cercle inscrit à ABC est le triangle médian, et a pour aire 1/4 de ABC
Le cercle circonscrit à abc et le cercle inscrit ont donc des rayons dans le rapport √(1/7)/(1/4) = 2/√7
l'ellipse abca'b'c' est donc homothétique de l'ellipse de Steiner intérieure dans le même rapport.
L'ellipse de Steiner extérieure est homothétique de l'ellipse intérieure dans le rapport 2 (-2 en fait), donc homothétique de l'ellipse abca'b'c' dans le rapport √7

Dans le triangle équilatéral, Gm² = GM² + Mm² = s²/12 + (s/6)² soit GM = s/3.
On obtient ainsi une autre ellipse qui passe par les 6 points aux tiers des côtés, homothétique de l'ellipse de Steiner dans le rapport  2/√3

Généralisation

On peut bien entendu effectuer une homothétie de centre G des ellipses de Steiner dans un rapport quelconque, ce qui conduit à des divisions des côtés en rapport quelconques, mais isotomiques (Bm = Cm'), et inversement pour toute division isotomique des côtés dans le rapport k = Bm/BC = Cm'/CB, on obtient deux ellipses homothétiques des ellipses de Steiner.
Resterait à exprimer le rapport d'homothétie en fonction de k, mais j'ai la flemme...

Un cas particulier intéressant est quand le rapport d'homothétie est 1.
C'est à dire quand abca'b'c' sont sur l'ellipse de Steiner même.

Transformons ABC en triangle équilatéral par la transformation affine précédente.
Dans ce triangle équilatéral Ac'GcB sont sur un même cercle pour toute valeur de k :
l'angle cAB = aBC = α donne dans le triangle AcB l'angle en c = π - α - (π/3 - α) = 2π/3
Le point c est donc sur le cercle de centre G' tangent en A et B aux côtés AC et BC
Comme dans le cas cherché l'ellipse est l'ellipse de Steiner, c'est à dire dans le triangle équilatéral le cercle abca'b'c' est le cercle inscrit, le point c est l'intersection du cercle inscrit et de ce cercle tangent en A et B.

Posons θ = l'arc cG. l'arc cB est alors π/3 - θ et donc l'angle BAc est (π/3 - θ)/2.
L'angle AmB est donc π - π/3 - (π/3 - θ)/2 = π/2 + θ/2 et on a k = Bm/BA = sin(π/6 - θ/2) / sin(π/2 + θ/2) = 1/2 - √3/2 tan(θ/2)
La droite cc' est l'axe radical de ces cercles, et coupe donc la tangente commune MB en son milieu i, soit au quart de BC. Donc Nh = NC/4 d'où G'h = (7/8)G'G et θ = arccos(7/8)
on en déduit tan(θ/2) = 1/√15 et

k =  (5 - √5)/10 ≈ 0.2763932...

Note : l'aire de abc est alors la même que celle du triangle médian, soit donc le quart de ABC.
Le rapport de division des côtés est donc celui obtenu dans le partage "non trivial" de ABC en 4 triangles de même aire.
On avait trouvé par une méthode directe BC/Bm = (5 + √5)/2, dont l'inverse est bien Bm/BC = 2/(5 + √5) = 2(5 - √5)/(5² - 5) =  (5 - √5)/10 = k

Les sommets du triangle d'aire 1/4 ABC sont sur l'ellipse de Steiner