Intersections imaginaires

On peut étendre le plan à des coordonnées imaginaires (plan "complexifié"). Alors une droite quelconque coupe toujours une conique quelconque en deux points, éventuellement confondus.
Simplement si la droite ne coupe pas (au sens usuel) la conique, ces points ont comme coordonnées des nombres complexes, non réels.
Par exemple le cercle (x-1)² + (y-2)² = 3 "coupe" la droite y = 0 en les points de coordonnées (1-i, 0) et (1+i, 0)

On s'intéresse ici à la construction géométrique des parties réelles et imaginaires des points "d'intersection".
On se place dans un repère où la droite donnée est l'axe Ox, il convient alors de construire les valeurs a et b des points d'intersection, d'abscisses non réelles OA = a + ib et OB = a - ib

Dans le cas du cercle, on peut obtenir une construction relativement simple :
Par symétrie, le diamètre perpendiculaire à Ox coupe Ox en M, milieu de AB, que ces points soient réels ou imaginaires,
on a donc OM = (OA + OB)/2 = a

Pour b, on peut considérer la puissance de M par rapport au cercle.
Soit MT, MT' les tangentes de M au cercle.
La puissance de M est MA.MB = (ib)(-ib) = b² = MT² = MT'²
b est donc la longueur des tangentes issues de M (M est extérieur puisque les intersections ne sont pas réelles).

On va s'intéresser maintenant au cas général d'une conique quelconque en position quelconque avec la droite Ox.
Le coup de la puissance n'est plus aussi simple...

Polaire

Rappelons que la polaire d'un point P est le lieu des conjugués harmoniques, réels ou imaginaires, de ce point. C'est à dire des conjugués harmoniques de P par rapport aux points d'intersection d'une sécante quelconque issue de P.

Considérons alors la polaire du point à l'infini de Ox.
Il s'agit en fait du "diamètre conjugué" de la direction Ox, lieu des milieux m des sécantes CD parallèles à Ox, puisque (∞, m, C, D) = -1 ⇔ m milieu de CD
Cette polaire coupe Ox au point M et (∞, M, A, B) = -1
C'est à dire que M est le milieu de AB, OM = ((a+ib) + (a-ib))/2 = a, comme pour le cercle, simplement le diamètre conjugué n'a aucune raison d'être perpendiculaire, il ne l'est que si les axes de la conique sont respectivement parallèles et perpendiculaires à Ox.
Reste à trouver b.

Considérons alors la polaire d'un point quelconque de Ox, par exemple O.
En tout cas différent de M, sinon on n'obtient pas une nouvelle relation, mais la même : M milieu de AB.
Soit U l'intersection de la polaire de O avec Ox. (O,U,A,B) = -1 et en prenant comme origine le milieu M : MA² = MB² = (±ib)² = -b² = MO.MU < 0
La construction de b est alors classique :
Tracer le cercle de diamètre OU. La demi corde perpendiculaire en M = b.

Rappelons la construction classique de la polaire de P (ici P = O) :
Tracer deux sécantes quelconques PCD et PEF.
CE et DF se coupent en I, CF et DE se coupent en J
IJ est la polaire de P.

Applet

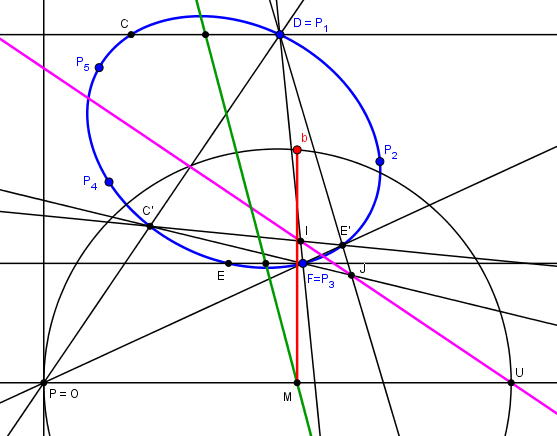
L'applet suivante effectue ces constructions à partir d'une conique définie par 5 points 1,2,3,4,5
Les points d'intersections de droites passant par ces 5 points sont alors facilement construits (à la règle seule) par le théorème de Pascal.
Les sécantes PC'D, PE'F et les parallèles à Ox   CD et EF sont ainsi choisies comme passant par des points définissant la conique (points 1 et 3).
Bien entendu les 5 points ainsi que O sont déplaçables à la souris.
L'applet ne gère pas les cas dégénérés qui peuvent se produire selon la position de O ou des 5 points, par exemple si O est sur la droite DF, les deux sécantes OC'D et OE'F sont confondues.
Dans la pratique, il sufirait de choisir dans ce cas là pour points D et F d'autres points que les points 1 et 3.

Nota : l'applet Géogebra triche largement (évitant la construction effective de Pascal) :
la droite IJ = polaire de O peut être obtenue directement par la commande Polaire(O, c) (et donne à rebours les points E et C !)
la droite reliant les milieux de CD et EF est le diamètre conjugué de Ox : commande Diamètre(Ox, c)

Intersections réelles

Cette construction permet aussi de construire les points d'intersection réels d'une conique définie par 5 points et d'une droite quelconque.
Dans ce cas les propriétés précédentes restent valables :
M est toujours le milieu de AB, et MA² = MB² = MO.MU
Ici MA et MB sont réels et donc MO.MU > 0
MA = MB est alors la longueur de la tangente de M au cercle de diamètre OU, M étant alors extérieur au cercle.
L'applet ci-dessus traite automatiquement ce cas, selon que M est extérieur (intersections réelles) ou intérieur (intersections imaginaires) au segment OU.

D'autres constructions possibles utilisent une homologie pour transformer la conique en un cercle, ou l'involution de Desargues sur la droite induite par le faisceau des coniques définies par 4 des points donnés. Voir Coniques pour les détails.