Isobarycentres

Le centre de gravité (isobarycentre) d'un quadrilatère plein (la surface du quadrilatère) n'est pas le même que le barycentre de ses sommets (4 points), ni le même que celui de ses côtés (quadrilatère en fil de fer).

Construire géométriquement chacun de ces barycentres.

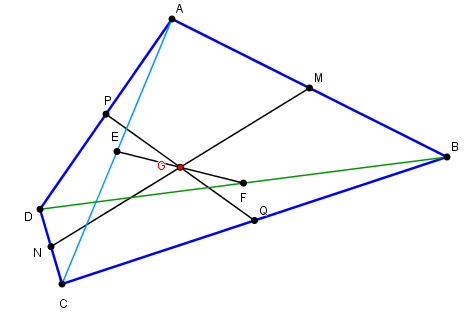
Centre de gravité des sommets

Le centre de gravité de A et B est au milieu m de AB
Le centre de gravité de C et D est au milieu n de CD
Le centre de gravité G de (A,B,C,D) est donc sur la droite mn
C'est le barycentre de m(2) et n(2), donc au milieu de mn.
On peut aussi associer différemment les sommets et donc G est sur la droite pq, p et q étant les milieux de AD et BC.

Les médianes d'un quadrilatère se coupent en leur milieu qui est l'isobarycentre des sommets

enfin la droite joignant les milieux des diagonales passe elle aussi par G.

Centre de gravité de la surface

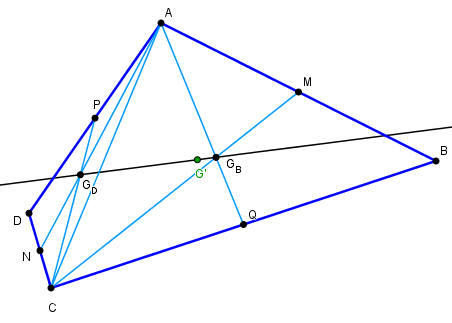Coupons le quadrilatère en deux triangles ABC et ACD, de centres de gravité G_b et G_d
Le centre de gravité G' du quadrilatère est sur la droite G_bG_d.
On peut le construire directement comme barycentre de G_b(Aire de ABC), G_d(Aire de ACD)
Les aires des triangles étant proportionnelles à leur hauteur (même base AC), ceci ne pose pas de difficulté insurmontable :
construction du point G' divisant G_bG_d dans le rapport des hauteurs opposées

Toutefois, il y a plus expéditif : recommencer la construction avec les triangles ABD et BCD, de barycentres G_a et G_c.
G' est alors l'intersection de G_bG_d et G_aG_c

Centre de gravité des côtés

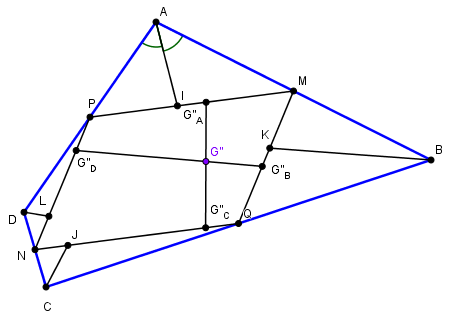Le centre de gravité d'un côté est bien sûr en son milieu.
Construisons le centre de gravité de AB+AD.
C'est à dire de m(AB) et p(AD), ou ce qui revient au même de m(Am) et p(Ap)
Ce barycentre divise le segment mp dans le rapport Ap/Am
Soit AI la bisectrice de l'angle A
I divise mn dans le rapport Am/Ap.
Le point G"_a symétrique par rapport au milieu de mn divise le segment dans le rapport inverse, et est donc le barycentre cherché.
On fait de même pour les côtés BC et CD, dont le centre de gravité est G"_b.
Le centre de gravité G" des côtés de ABCD est donc sur la droite G"_aG"_b
En recommençant avec un autre groupement des côtés (AB,BC) et (AD,CD), G" est aussi sur G"_cG"_d, donc l'intersection de G"_aG"_b et G"_cG"_d

Triangle

Il est "bien connu" que le centre de gravité d'un triangle plein est le même que celui de ses sommets (encore faut-il le prouver).
Par contre le centre de gravité des côtés (triangle en fil de fer) est différent.
Construisons le...

Les centres de gravité de AB et AC sont les milieux N et P des côtés.
Le centre de gravité de (AB,AC) est donc comme ci-dessus le point k, symétrique de j par rapport au milieu m de NP, j étant le pied de la bisectrice de <)NAP.
Le centre de gravité cherché est donc situé sur la droite Mk.
Celle-ci est parallèle à la bisectrice de l'angle A : droite des milieux dans AJK.
Donc Mk est bisectrice du triangle MNP.

Le centre de gravité du triangle en fil de fer est le centre du cercle inscrit dans le triangle médian

Ce point s'appelle le point de Spieker S du triangle ABC.
Le triangle médian est homothétique de ABC dans l'homothétie de centre G (isobarycentre des sommets de ABC) et de rapport -1/2,
le centre de gravité G, le centre du cercle inscrit I et le point de Spieker S sont donc alignés et

GI> = -2 GS>

S est aussi le milieu du segment INa, où Na est le point de Nagel de ABC, intersection des droites joignant les sommets aux points de contact des cercles exinscrits.