Points circonscrits

Construire un triangle étant données les intersections avec le cercle circonscrit :
- des hauteurs
- ou des bisectrices
- ou des médianes

Hauteurs

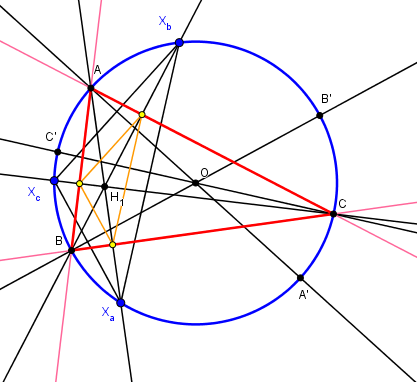
Les points donnés sont les symétriques de l'orthocentre par rapport aux côtés.
Le triangle orthique de ABC est donc (droite des milieux) homothétique du triangle XaXbXc donné dans le rapport 1/2, de centre H. OA étant perpendiculaire au coté du triangle orthique est aussi perpendiculaire à XbXc, d'où la construction.
La perpendiculaire en O à XbXc coupe le cercle circonscrit en A et A'
La perpendiculaire en O à XaXc coupe le cercle circonscrit en B et B'
et les 4 solutions ABC, AB'C', A'BC', A'B'C
Pour chacune, l'orthocentre est l'intersection des hauteurs AXa et BXb, et C est le second point d'intersection de HXc avec le cercle circonscrit.
Cet orthocentre est le centre d'un cercle inscrit ou exinscrit à XaXbXc.
Autre méthode : les sommets A,B,C sont les milieux des arcs XbXc, XcXa, XaXb.

Bissectrices

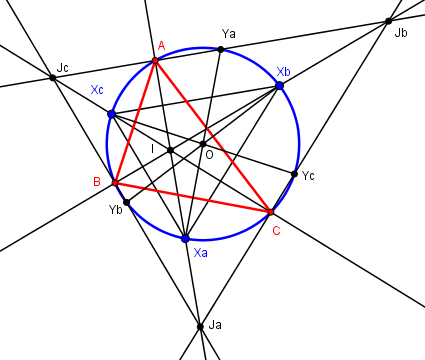Les points donnés sont les milieux des segments reliant le centre du cercle inscrit aux centres des cercles exinscrits. Xb milieu de IJb et Xc milieu de IJc.
XbXc est donc parallèle (droite des milieux) à JbJc. Par conséquent perpendiculaire à la bissectrice AXa.
D'où la construction : la perpendiculaire à XbXc issue de Xa recoupe le cercle en A etc.

Les intersections des bissectrices extérieures avec le cercle circonscrit étant bien entendu les points diamétralement opposés aux points donnés, la droite JbJc est la parallèle à YbYc en Ya.
Ceci donnant la variante si les points donnés sont des intersections Ya,Yb,Yc avec les bissectrices extérieures.

Médianes

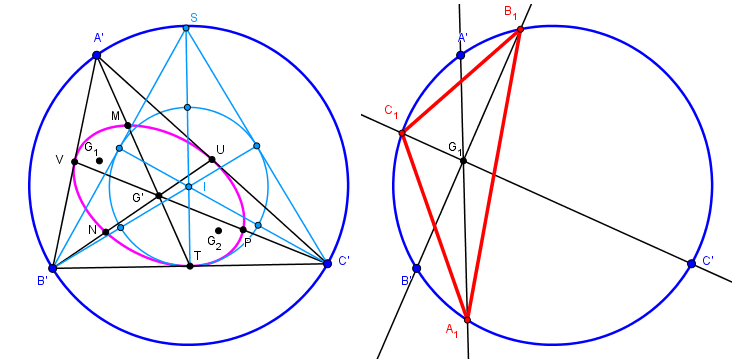
La véritable difficulté est ici...

On démontre que les solutions sont données par les foyers de l'ellipse de Steiner du triangle A'B'C', tangente au côtés de A'B'C' en leur milieu.
Ces foyers G1 et G2 sont les centres de gravité des triangles solution A1B1C1 et A2B2C2.
Il "suffit" donc de construire les foyers de cette ellipse par des méthodes classiques.

Le centre de l'ellipse est le centre de gravité G' de A'B'C' et l'ellipse est tangente aux côtés en leur milieux TUV Ceci suffit à définir cette ellipse.
En considérant la figure comme la transformée par affinité (qui conserve les milieux) du cercle inscrit dans un triangle équilatéral B'C'S, on en déduit que cette ellipse passe par les milieux de G'A', G'B' et G'C'
Donc la construction immédiate de cette ellipse par 5 points (et même 6)
On peut alors tricher en demandant directement à Geogebra de tracer ses foyers !!
sinon il y faudra (à la règle et au compas) un peu plus d'efforts, il y a de nombreuses façons de construire ces foyers.

compléments sur l'ellipse de Steiner