Intersection de coniques

Les intersections de deux coniques ne sont en général pas constructibles à la règle et au compas, car résultant en une équation générale du 4ème degré.
Les cas suivants sont constructibles, l'équation du 4ème degré se décomposant en équations du second degré constructibles.

Même centre

Il suffit de déterminer les coniques dégénérées du faisceau défini par les deux coniques données.
Nous définissons ici les deux coniques par leurs foyers F et F' et un cercle directeur (F),
Les points de contrôle dragables dans l'applet sont en fait le centre O, le sommet S et le foyer F.
Le cercle directeur et l'autre foyer s'en déduisant de façon élémentaire.

Rappelons quelques constructions de base.

Construction d'un point courant de la conique

Soit m un point courant du cercle directeur (F).
La droite Fm et la médiatrice de F'm se coupent en M sur la conique, de plus la médiatrice de F'm est la tangente en M à la conique.
Rappelons ici la propriété importante : M est le centre d'un cercle passant par F' et tangent au cercle directeur (F). Cette propriété pouvant servir de définition de la conique : lieu des centres des cercles etc.

Construction de l'intersection avec une droite (d) quelconque

Ceci revient à chercher sur la droite le centre d'un cercle passant par F' et tangent à (F)
Il passe alors par le symétrique F1 de F' par rapport à cette droite.
On est ainsi ramené à construire un cercle passant par F' et F1 et tangent à (F), problème d'Apollonius 'PPC'.
Traçons un cercle quelconque passant par F' et F1 donc centré sur (d), et coupant (F) en A et B. Les droites F'F" et AB se coupent en I. Soit IT une tangente à (F) issue de I. Le cercle cherché est le cercle circonscrit à F'F1T, son centre est donc l'intersection de (d) et de la médiatrice de F'T, ou même plus simplement ici de (d) avec FT.
Le choix d'un cercle "quelconque" est ici fait manuellement, le point D définissant la droite (d) servant de centre de ce cercle. A choisir donc "extérieur" à la conique pour que ce cercle coupe le cercle directeur.
La construction échoue si (d) est la droite FF', mais alors la construction des sommets est bien plus simple !
L'applet ne cherche pas à construire ce cas particulier par une construction conditionnelle, les sommets étant déja tracés.

Diamètre conjugué d'un diamètre donné

On applique la propriété caractéristique : on trace une sécante quelconque parallèle à (d) coupant la conique en P et P',
Le diamètre conjugué passe par le milieu de PP' et le centre de la conique.
Ici la sécante "quelconque" est la droite précédente car on en a deja les intersections.
Si elle ne coupe pas la conique, ou si elle passe par le centre, il faudrait en choisir une parallèle
Le diamètre conjugué passe aussi par l'intersection J des tangentes en les points d'intersection, qui sont les médiatrices de TF et de T'F'
Ou parallèle à ces tangentes si la droit passe par le centre
Ces différents cas compliqueraient l'applet et ne sont pas traités

Armé de ces constructions élémentaires, que nous ne détaillerons plus, cherchons l'intersection de nos deux coniques.
Comme elles ont même centre, par symétrie les points d'intersection forment un parallélogramme (les diagonales se coupent en leur milieu O).
Les côtés de ce parallélogramme sont des directions conjuguées pour chacune des deux coniques.
Soit (d) un diamètre quelconque (d') le diamètre conjugué de (d) par rapport à la première conique Γ, et (d") le diamètre conjugué de (d') par rapport à la seconde conique Γ_b.
On définit ainsi (step 1) une homographie (d) → (d") du faisceau de droites O* : droite vert (d) → droite orange (d")
Les directions des côtés du parallélogramme seront les directions fixes de cette homographie.
Ils sont construits en projetant (d) → (d") sur un cercle passant par O, l'axe de l'homographie sur le cercle coupe celui ci en les points fixes.
Pour cela (step 2) on choisit trois points quelconques a,d,c et leur transformés a",d",c", et on applique la définition de l'axe : lieu des points d'intersection de ad" et a"d.
Les points choisis sont (a) axe focal de Γ, le conjugué est l'axe transverse et (a") est le conjugué de cet axe transverse par rapport à Γ_b
On fait de même avec (c) l'axe transverse de Γ et (c") le conjugué de l'axe focal de Γ par rapport à Γ_b
Enfin (d) et (d") sont un point courant, défini par une droite dragable via le point vert d.

On obtient ainsi les directions (magenta) Ou, Ov des côtés du parallélogramme.
Il n'est pas aussi simple de construire maintenant les côtés eux même.

Choisissons (step 3) une droite (L) quelconque coupant les deux coniques en (M, M') et (M_b, M'_b)
Le faisceau des coniques déterminé par Γ et Γ_b définit sur (L) une involution de Desargues parfaitement définie par M ↔ M' et M_b ↔ M'_b
Si cette involution est hyperbolique, elle possède deux points fixes réels I et J.
Pour cela il suffit de choisir (L) pour que l'une des cordes MM' ou M_bM'_b soit strictement intérieure à l'autre.
Enfin pour effectuer une construction effective, il est nécessaire que ces points fixes ne soient pas rejetés à l'infini, donc que (L) ne soit pas parallèle aux diamètres conjugués construits précédemment.
Cela laisse tout de même un large choix pour (L).
Dans l'applet (L) est définie par les deux points "courants" M et M_b des deux coniques. (pilotés par les points cyan des cercles directeurs).
Construisons donc (step 4) les points fixes de cette involution, ce que l'on obtient facilement en la projetant sur un cercle quelconque, celui défini précédemment faisant l'affaire.
L'axe de l'involution sur le cercle est construit : passant par les intersections de mm_b avec m'm'_b et mm'_b avec m'm_b
Ses intersections avec le cercle donnent I et J après reprojection sur (L).
L'involution M ↔ M' sur (L) est alors caractérisée par (M,M',I,J) = -1, division harmonique.
Soit Q l'intersection avec (L) du diamètre Ou et E,E' les intersections avec la conique dégénérée cherchée, constituée des deux cordes communes parallèles à Ou.
Q est évidemment le milieu de EE' et ainsi on peut construire (step 5) E et E' par QE² = QE'² = QI.QJ
On obtient ainsi les cordes communes comme parallèles à Ou passant par E et E', puis les intersections de ces cordes avec Γ (ou avec l'autre conique dégénérée parallèle à Ov, construite de la même façon).

Avertissement :
Le choix des "points quelconques" influe sur la construction.
Si on change les coniques, il faut parfois changer (manuellement) ces points de construction :

La construction échoue même complètement si les deux coniques ont les mêmes axes :
il faudrait choisir une deuxième droite quelconque pour l'étape 1.
De toute façon dans ce cas la construction est plus simple : les directions fixes sont les axes !
Un choix automatique de ces points de contrôle conduirait à une figure généralement non représentative (tous les points ou presque en dehors de la figure) et compliquerait encore la construction (165 éléments géométriques construits)
La simple construction d'une intersection ou d'un conjugué nécessite déja plusieurs éléments comme indiqué dans les constructions préliminaires.
Même pour simplement projeter la direction (d) sur le cercle cela nécessite deux éléments ! La simple intersection de (d) avec le cercle ne suffisant pas : il faut garantir que c'est l'autre point que O etc.
Alors que manuellement c'est "évident", ce n'est pas aussi simple dans une applet automatique, il faut souvent effectuer des constructions artificielles, par exemple ici c'est le symétrique de O par rapport à la perpendiculaire à (d) issue du centre w.

Autre méthode

La construction précédente échoue en fait systématiquement si les deux coniques sont des hyperboles avec seulement deux points d'intersections réels.
En effet, dans ce cas le parallélogramme considéré alors n'est pas réel.
La méthode suivante est due paraît-il à Chasles et construit la 3ème conique dégénérée : celle des deux diagonales.

Considérons le faisceau de coniques défini par les deux coniques considérées.
Les polaires d'un point par rapport aux coniques du faisceau passent par un point fixe. On construit donc les polaires de deux points M et N par rapport à chacune des deux coniques
Les polaires de M se coupent en M' qui est le point fixe des polaires de M par rapport à toutes les coniques du faisceau
Et de même pour N'
Ceci définit une involution de (O*) des droites OM ↔ OM'
Les droites fixes de cette involution sont la conique dégénérée cherchée.
Construction même plus simple que l'autre !

Rappelons la construction d'une polaire :
Deux sécantes quelconques MM₁M₂ et MM₃M₄ (ici passant par les foyers pour être certain qu'elles coupent la conique)
Les droites M₁M₄ et M₂M₃ se coupent en I
Les droites M₁M₃ et M₂M₄ se coupent en J
La polaire est la droite IJ

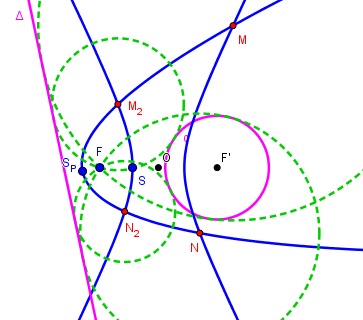
Un foyer commun

La conique étant définie comme lieu des centres des cercles passant par un foyer et tangents au cercle directeur (ou à la directrice pour une parabole) le problème se ramène au problème d'Apollonius dans le cas PCC : un point (le foyer commun) et deux cercles (les deux cercles directeurs) ou bien PDC (une parabole, la directrice) ou bien PDD (deux paraboles, les directrices).
Illustration avec une parabole, définie par Foyer F et sommet S_P, et une conique à centre O (ellipse ou hyperbole) définie par le même foyer et le sommet S

Un axe commun

Analytiquement, l'équation du 4ème degré devient une simple équation du second degré, donc constructible.

Là aussi la clé est la construction d'une conique dégénérée et l'involution de Desargues.

Détails

Points connus

Si deux points d'intersection sont déja connus, les deux autres peuvent être construits.
La construction peut même se faire à la règle seule si trois points sont connus, ou si une des coniques est un cercle.
Cette construction a été vue ici