Points circonscrits

Construire un triangle ABC étant données les intersections A'B'C' des médianes avec le cercle circonscrit.

On démontre que les solutions sont données par les foyers de l'ellipse de Steiner du triangle A'B'C', tangente au côtés de A'B'C' en leur milieu.
Ces foyers G1 et G2 sont les centres de gravité des triangles solution A1B1C1 et A2B2C2.
La démonstration est exposée plus tard, mais déja l'applet suivante effectue la construction de ces foyers>

Le centre de l'ellipse est le centre de gravité G' de A'B'C' et l'ellipse est tangente aux côtés en leur milieux TUV Ceci suffit à définir cette ellipse.
Déterminons déjà les axes. Les médianes et les côtés du triangle médian TUV sont des directions conjuguées, et nous chercherons les axes en tant que diamètres conjugués perpendiculaires
Pour cela utilisons l'involution définie par deux paires de diamètres conjugués du faisceau G'* des droites passant par G', en projetant cette involution sur un cercle passant par G'.
Le pôle I de cette involution est l'intersection des droites reliant les points homologues sur le cercle.
Une paire de diamètres conjugués perpendiculaires G'x, G'y, c'est à dire les axes de l'ellipse, est obtenue par les intersections avec ce cercle du diamètre xy passant par I.
Une fois qu'on a les axes, construire les foyers est assez simple.
Nous utilisons la propriété que les tangentes et les normales à l'ellipse sont les bissectrices des rayons focaux.
en d'autres termes, si M et N sont les intersections avec l'axe de la tangente (B'C') et de la normale (perpendiculaire à B'C' au point de contact T), (M,N,G1,G2) est une division harmonique.
G' étant le milieu de G1G2, cela se traduit par G'G1² = G'G2² = G'M.G'N
G'G1 est donc égal à la tangente issue de G' au cercle de diamètre MN.
Ceci montre lequel est l'axe focal: celui pour lequel M et N sont du même côté de G'.

A',B',C' draggables définissent les points donnés sur le cercle.
Le point jaune w définit le cercle quelconque passant par G'.
L'applet donne un résultat aberrant lorsque A'B'C' est isocèle en A (pour cause d'axe parallèle ou perpendiculaire à B'C'), il faudrait alors effectuer la construction des foyers (step 2) à partir d'un autre côté, ce que ne sait décider l'applet par elle-même.
Si A'B'C' est équilatéral, les deux solutions sont confondues en une seule, l'ellipse de Steiner devenant le cercle inscrit.

Une construction directe de l'axe de l'ellipse de Steiner utilise la propriété suivante :
Les axes sont parallèles aux asymptotes de l'hyperbole de Kiepert.
Ces asymptotes sont les droites de Simson des intersections S et S' de OK avec le cercle circonscrit, où K est le point de Lemoine de A'B'C'.
Il suffit en fait de tracer deux symmédianes pour avoir K et deux projections de S sur les côtés de A'B'C' pour avoir la droite de Simson.
On peut aussi utiliser d'autres constructions que la définition même du point de Lemoine pour le construire.
Par exemple, ici les symmédianes sont les droites reliant les sommets du trinagle aux sommets du "triangle tangentiel" A_tB_tC_t
Une fois obtenus les axes de l'ellipse, la suite comme précédemment.
Une telle construction évite d'avoir à choisir un cercle arbitraire.

D'autres constructions

des foyers et axes de l'ellipse de Steiner :
Une construction directe des foyers, basée sur la formule donnant la longueur de l'axe de l'ellipse de Steiner, c'est à dire directement le rayon du cercle principal.
Des calculs relativement compliqués sont à l'origine de cette construction.
Construisons A' et A'' avec les triangles A'BC et A''BC équilatéraux.
Alors le rayon du cercle principal est (AA + AA'')/6 (c'est là le résultat génial de ces calculs)
Et la construction :
Ce cercle est tracé, il coupe les côtés en 6 points, qui forment les triangles podaires des deux foyers.
Les perpendiculaires aux côtés en ces points se coupent donc par trois en les foyers F1 et F2.
Ce qui donne les axes.

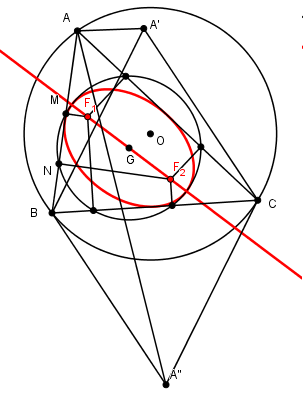
Il faut choisir les points pour avoir les intersection en Fi de trois perpendiculaires)
Ce choix, facile "à la main", est un peu compliqué dans une applet et il vaut mieux avoir l'axe d'abord !
Comme on l'a vu précédemment, on peut les obtenir via le point de Lemoine K et l'axe de Brocard (OK)
Mais aussi via les points de Steiner S et de Tarry T :
Le petit axe est la bissectrice de l'angle ∠KGS ou de l'angle ∠OGT, (et l'axe focal celle de ∠ZGO, voir plus loin)

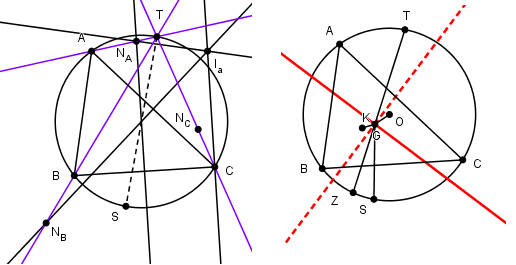
La façon la plus efficace d'obtenir ces points S et T est d'obtenir T d'abord :
C'est l'intersection des droites joignant les sommets aux points de Neuberg correspondants, centres des cercles de Neuberg, facile à construire.
La perpendiculaire en C à BC coupe la médiatrice de AC en Ib
La médiatrice de BC et la perpendiculaire par Ib = AB se coupent en Na, centre du cercle de Neuberg associé à la base BC.
Et de même avec les deux autres Bc et Nb
Le point de Tarry est alors l'intersection des droites ANa, BNb et CNc (deux suffisent pour le construire)
Ce point est sur le cercle circonscrit, et le point de Steiner lui est diamétralement opposé.

Une autre :
Soit Z l'intersection des symétriques de (OG) par rapport aux côtés du triangle
(ce point est sur le cercle circonscrit)
Les bissectrices de l'angle ZGO sont les axes de l'ellipse
Soit O' l'intersection de ZG avec la parallèle de O à la bissectrice intérieure
Le cercle SOO' recoupe cette bissectrice en les foyers G1 et G2

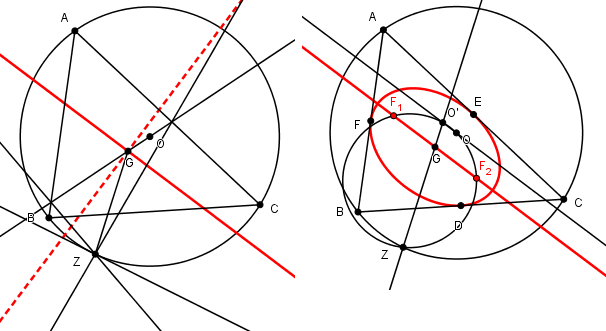
(applet commune regroupant toutes ces constructions directes)

Démonstrations

Considérons l'affixe z = x+iy de G, et étant données les affixes a,b,c de A'B'C', dans un repère arbitraire.
L'inversion de centre G, centre de gravité de ABC, qui échange A↔A', B↔B' et C↔C' (laissant globalement inchangé le cercle circonscrit) s'exprime par les relations, où k est la puissance de G par rapport au cercle circonscrit :

GA^> = kGA'^>/|GA'|² etc. avec B et C. Enfin GA^> + GB^> + GC^> = 0 se traduit par :

GA'^>/|GA'|² + GB'^>/|GB'|² + GC'^>/|GC'|² = 0, soit sur les affixes, en notant z le conjugué de z, en rappelant que |u|² = u.u et après simplification :

1/(z - a) + 1/(z - b) + 1/(z - c) = 0, ou encore en prenant les conjugués :

1/(z - a) + 1/(z - b) + 1/(z - c) = 0

Soit, en posant S = a + b + c et P = ab + bc + ac :
(z - a)(z - b) + (z - a)(z - c) + (z - b)(z - c) = 3z² - 2Sz + P = 0

On en déduit l'existence de deux solutions G1 et G2, d'affixes z1 et z2 racines de ce polynome.

Le milieu de G1G2 : (z1 + z2)/2 = S/3 est donc le centre de gravité G' de A'B'C', d'affixe (a + b + c)/3

D'autre part on peut écrire les deux identités conjuguées :

(z - a)(z - b) + (z - a)(z - c) + (z - b)(z - c) = 3(z - z1)(z - z2)

(z - a)(z - b) + (z - a)(z - c) + (z - b)(z - c) = 3(z - z1)(z - z2)
et en mettant z = a :

(a - b)(a - c) = 3(a - z1)(a - z2)

(a - b)(a - c) = 3(a - z1)(a - z2)

soit (a - b)/(a - b) × (a - c)/(a - c) = (a - z1)/(a - z1) × (a - z2)/(a - z2)

Mais (u - v)/(u - v) = e^2iθ où θ est l'angle de u-v avec l'axe réel.
L'équation ci-dessus exprime alors que B'A'C' et G1A'G2 ont les mêmes bisectrices. De même avec les autres sommets B' et C'.
Donc G1 et G2 sont conjugués isogonaux.

Théorème (bien connu*) : deux points conjugués isogonaux sont les foyers d'une conique tangente aux côtés du triangle.
Le centre de cette conique étant le milieu de G1G2, est ici le centre de gravité G' de A'B'C'.
Cette conique est donc l'ellipse de Steiner inscrite dans A'B'C', tangente aux côtés en leur milieu.

Ceci se montre facilement en remarquant que la médiane A'T passe par le milieu de la corde des deux autres points de contact UV.
A'T est donc un diamètre et passe par le centre de la conique tangente aux côtés en leur milieu. Le centre de l'ellipse de Steiner est donc le centre de gravité, et réciproquement (puisqu'il y a une seule conique de centre donné tangente aux côtés)

*) La démonstration que deux conjugués isogonaux P,Q sont les foyers d'une conique tangente aux côtés se trouve dans la littérature. Un plan de démonstration possible est donné ici à titre d'exercice :
- Montrer que les triangles podaires de P et Q ont même cercle circonscrit, de centre le milieu de PQ (cercle podaire) de rayon r.
- Soit R1,R2,R3 les symétriques de P par rapport aux côtés de ABC.
   Montrer que R1R2R3 sont sur le cercle Γ de centre Q de rayon 2r
- QR1 etc. coupent les côtés de ABC en U,V,W. Montrer que la conique de foyer P et Q et de cercle directeur Γ est tangente aux côtés en U,V,W.

Annexe

Construction générale de conjugués isogonaux P,Q de milieu donné O.
La difficulté est ici de trouver les points de contact UVW, car la suite est comme pour la première construction avec l'ellipse de Steiner : diamètres conjuguées etc...

La droite AO étant un diamètre, coupe la corde VW en son milieu (propriétés des polaires, O est le pôle de la droite de l'infini) .
La direction de VW est conjuguée de la direction AO et on est amené à construire un triangle inscrit UVW, la direction de ses côtés étant connue.
De O traçons le parallélogramme OV'AW', OA coupe V'W' en son milieu et V'W' est la direction cherchée de VW.
On obtient de même les directions de UV et UW.
La construction d'un triangle U'V'W', V' et W' étant sur AB et AC s'en déduit immédiatement.
AU' coupe BC en U cherché (homothétie de centre A, U'V'W'→UVW)
Selon la position de O, la conique est une hyperbole ou une ellipse.
Les régions sont délimitée par le triangle médian de ABC (en prolongeant ses côtés)

Le point w choisit le cercle arbitraire pour projeter l'involution de O*
L'applet ne comporte pas de précaution particulière quand la construction dégénère : axe parallèle à BC, conique dégénérée en droite ou en cercle...

Preuve élémentaire

La démonstration suivante n'utilise ni les affixes ni explicitement l'ellipse de Steiner.
Bien que plus compliquée, elle n'utilise donc que des connaissances de base.

Lemme

La projection orthogonale K'L' d'un segment quelconque KL sur la droite BC est donnée par K'L' = |KC² - KB² - (LC² - LB²)| / (2BC)

Démonstration : Soit M le milieu de BC, et f(K) = KC² - KB² = (KC^> - KB^>) (KC^> + KB^>) = 2BC^>.KM^>
|f(K) - f(L)| = |2BC^>KM^> - 2BC^>LM^>| = |2BC^>(KM^> - LM^>)| = |2BC^>.KL^>| = |2BC^>.K'L'^>| = 2a.K'L'

Théorème

Soit G le centre de gravité de ABC et A'B'C' le triangle circumcévien de G (intersections des médianes avec le cercle circonscrit), alors le cercle podaire de G par rapport au triangle A'B'C' a pour centre le centre de gravité G' de A'B'C'. (Cercle passant par les projections de G sur les côtés de A'B'C')

Démonstration :

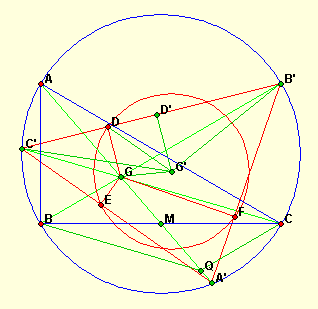
Soit a, b, c et a', b', c' les côtés de ABC et A'B'C'
Soit x, y, z et x', y', z' les distances respectives de G, G' aux sommets de ABC, A'B'C', c'est à dire x = AG, x' = A'G',...

Pour prouver que G' est le centre du cercle circonscrit au triangle podaire de G dans A'B'C' il suffit de prouver que la distance G'D, où D est la projection de G sur B'C', est une expresssion symétrique en x, y, z.
On rapelle les relations classiques x² = (2b² + 2c² - a²) / 9 et a² = 2y² + 2z² - x².
On obtient ces relations à partir de AG^> = (2/3)AM^>, en developpant et additionnant BC^>² = (AC^> - AB^>)² et (2AM^>)² = (AB^> + AC^>)²
Soit 9x² = b² + c² - 2AB^>.AC^> et a² = b² + c² + 2AB^>.AC^> , soit 9x² + a² = 2b² + 2c²
Puis en éliminant b et c entre les relations donnant x,y,z pour obtenir l'autre relation.

Soit Q le symétrique de G par rapport à M, milieu de BC.
GBQC est un parallélogramme donc QC = BG, GQ = 2GM = AG et ainsi le triangle BGQ a pour côtés x,y,z.
L'aire de ABC est trois fois l'aire Δ de BGQ = aire(BGC), soit Δ = abc / 12R (R étant le rayon du cercle circonscrit).

La puissance P de G est -P = AG.GA' = AG.(GM + MA') = AG.GM + (2/3)AM.MA' = x²/2 + a²/6 = (x² + y² + z²)/3.
(AM.MA' = -Puissance de M = -MB.MC = a²/4)

GB.GB' = GC.GC', les triangles GBC et GC'B' sont donc semblables et a'/a = GC'/BG = (CG.GC')/(BG.CG) soit a' = -aP/yz, et de même pour b' et c'.

Soit D' la projection de G' sur B'C' et h la hauteur issue de A' du triangle A'B'C', alors h = 3G'D' et comme b'c' = 2Rh, on obtient
G'D' = b'c'/6R = bcP²/(6Rx²yz) = 2P²Δ/ax²yz soit
(G'D')² = P⁴.(x+y+z)(y+z-x)(z+x-y)(x+y-z) / 4(ax²yz)² (1).

Le lemme donne pour la projection DD' de GG' :
f(G) = GC'² - GB'² = P²/z² - P²/y² = P²(1/z² - 1/y²)(puisque par définition P = GC'.GC)
f(G') = G'C'² - G'B'² = z'² - y'² = (2a'² + 2b'² - c'²)/9 - (2a'² + 2c'² - b'²)/9 = (b'² - c'²)/3 = P²b²/3x²z² - P²c²/3x²y² = (P²/3)((2x² + 2z² - y²)/x²z² - (2x² + 2y² - z²)/x²y²) = (P²/3)(2/z² - 2/y² - y²/x²z² + z²/x²y²) =
Par conséquent
DD'² = [(f(G) - f(G'))/2a']² = P⁴(y² - z²)² / 4(ax²yz)² (2)

de (1) , (2) et (G'D)² = (G'D')² + (DD')², on tire G'D = P² / 2xyz et le CQFD puisqu'une permutation de x,y,z donne la même valeur pour G'E et G'F.

Pour obtenir une construction effective à partir de cette démonstration, il reste à exprimer G'D en fonction de A'B'C' uniquement.