Ellipse
 D'après un problème posé par JC Arbaut sur fr.sci.maths
D'après un problème posé par JC Arbaut sur fr.sci.maths
Soient encore les droites D1 et D2, orthogonales à (AB) et passant respectivement par A et B.
Soit un point M sur le cercle C (draggable dans l'applet).
Tracer AM qui coupe D2 en P. Tracer BM qui coupe D1 en Q.
Tracer la perpendiculaire à (AB) passant par M, qui coupe (PQ) en N.
Alors lorsque M décrit le cercle C, le point N décrit une
ellipse, et PQ est la tangente en N à cette ellipse.
Soit H le pied de la perpendiculaire en M.
Soient U et V les milieux de AQ et BP.
L'homothétie AUQ → PVB (dans cet ordre) a pour centre le point commun aux droites
AP, UV et BQ, c'est à dire M.
M est donc le milieu de HN (Thales)
N est alors l'image de M dans l'affinité orthogonale de rapport 2, de droite fixe AB.
L'image du lieu de M (le cercle) est donc une ellipse lieu de N, de petit axe AB et
de grand axe = 2AB
Son excentricité est donc c/a = √3/2,
avec c² = a² - b², a = 2R, b = R
Les foyers sont les sommets des triangles équilatéraux de base AB.
Si H est en O, PQ // UV // AB et PQ tangente à l'ellipse en N est évident.
Sinon, soit I l'intersection de PQ avec AB.
I est le centre de l'homothétie AUQ → BVP et est donc sur UV.
La division (A,B,H,I) est alors harmonique et OH.OI = OA² = OB² = OM²
Le triangle OIM, de hauteur MH, est donc rectangle en M et UV est la tangente en M au cercle.
Son image QP par l'affinité orthogonale est donc la tangente en N à l'ellipse.
Tracer la droite (OM) coupant D1 en R (sauf pour deux positions de M sur le cercle bien sûr). Alors BR est perpendiculaire à PQ.
Les triangles AOR et AUI sont semblables, donc les triangles ABR et AQI aussi,
et finalement les triangles OBR et UQI.
Les angles ORB et UIQ sont donc égaux, et l'angle des droites (RB, IQ) est égal à celui des droites
(OR, UI) = π/2.
Extension
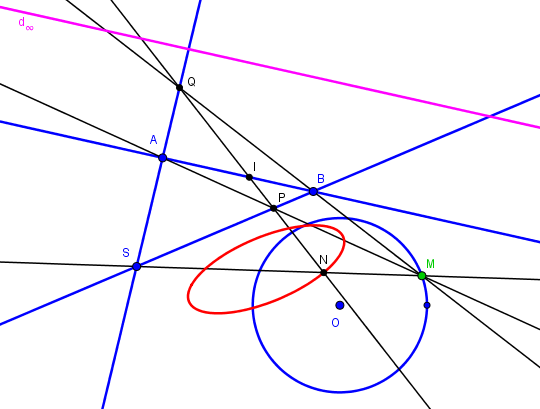
Soit deux droites SA et SB, et un cercle (C) quelconques.M un point du cercle. AM coupe SB en P, BM coupe SA en Q, SM coupe PQ en N
N décrit une conique quand M parcourt le cercle
Dans l'applet A,B,S,O sont draggables, de même que le point cyan définissant le rayon du cercle.
M est draggable sur le cercle.
Soient H l'intersection de SM et AB, soit I l'intersection de PQ et AB
Alors la division (S,M,N,H) = -1 est harmonique (construction et propriété
classique du quadrilatère complet et de ses diagonales).
Par conséquent le birapport (S,H,M,N) = 2, et N est le transformé de M dans
l'homologie projective de centre S et de droite fixe (axe) AB.
Quand M décrit une conique (le cercle) N décrit donc une conique.
Soit (D) la droite homothétique de AB de centre S et de rapport 2 (en magenta dans l'applet).
La transformée de D dans l'homologie est la droite de l'infini, et donc les points à l'infini
de la conique lieu de N sont les transformés des intersections de D avec le cercle.
Si D coupe le cercle, la conique est une hyperbole, si D est tangente au cercle, c'est une parabole,
si D ne coupe pas le cercle, c'est une ellipse.
Le problème précédent est le cas particulier où S est à l'infini et SA,SB sont tangentes en A et B au cercle.
De façon générale si SA et SB sont tangentes en A et B au cercle,
en appliquant le théorème de Brianchon (sous une forme réciproque) à l'hexagone ASBPNQ,
les "deux" côtés NP et NQ de cet hexagone sont tangents à la conique.
Sinon (SA et SB quelconques) PQ n'est pas tangente à la conique en général,
sauf peut-être pour certains points M particuliers :
PQ est l'image de IM dans l'homologie, et donc PQ sera tangente à la conique ssi IM est tangente au cercle.
Ce qui se produit ... parfois.