Point de Soddy
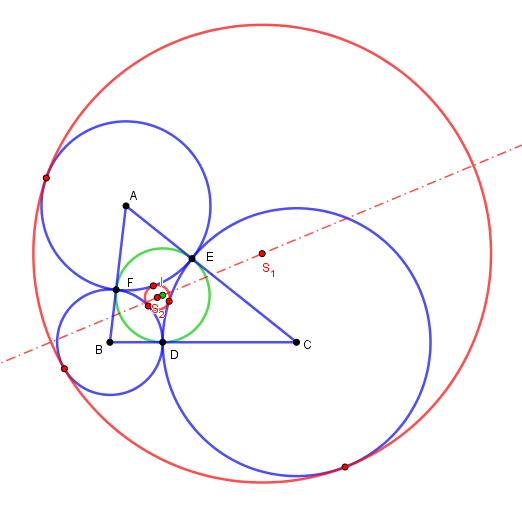
Etant donné trois cercles (A) (B) (C) mutuellement tangents, il existe généralement deux autres cercles qui leur sont tangents.Inversement on peut se demander si étant donné un triangle ABC quelconque, on peut trouver 3 cercles de centres A, B et C mutuellement tangents. La réponse est oui.
La 4ème roue du carosse (le 4ème cercle) est alors le cercle de Soddy du triangle ABC, et son centre le point de Soddy.
Il existe donc en général deux solutions, baptisées "Cercle (et point) de Soddy intérieur" pour celui qui est à l'intérieur du triangle curviligne déterminé par les 3 cercles (A) (B) (C), donc forcément à l'intérieur du triangle ABC.
Et "Cercle (et point) de Soddy extérieur" pour l'autre. A noter que c'est le cercle qui est extérieur. Son centre peut très bien être intérieur au triangle ABC
La droite joignant les deux points de Soddy est la Droite de Soddy
Les tangentes communes en D, E, F sont les axes radicaux de ces cercles deux à deux,
elles sont donc concourantes en un point I, centre radical de ces cercles.
ID = IE = IF et ces droites étant perpendiculaires aux côtés de ABC, I est le centre du cercle inscrit et
DEF les points de contacts
D'où l'existence et l'unicité des trois cercles mutuellement tangents extérieurement
(voir annexe pour des cercles tangents intérieurement)
Construction des points de Soddy
Considérons l'inversion de pôle E conservant le cercle (A).
Les cercles (B) et (C) sont transformés en deux droites perpendiculaires
à BC et tangentes au cercle (A') = (A), image de (A).
L'image du cercle (P) est donc un cercle (P') tangent à ces deux droites en V' et W', et à (A') en U'.
Donc un cercle égal à (A) dont le centre P' est sur la perpendiculaire en A à BC, avec U'P' = AU'.
Il existe deux cercles solutions. (P') correspond au cercle de Soddy extérieur cherché (P).
L'autre (P") est l'image du cercle de Soddy intérieur.
Le point de contact U de (P) avec (A) est l'image de U' et est donc sur EU'.
De même pour les points de contacts V et W avec (B) et (C).
Enfin P, E et P' sont alignés puisque les cercles (P) et (P') sont inverses l'un de l'autre.
D'où une construction du point de Soddy extérieur :
On construit les points de contact DEF du cercle inscrit, et le cercle (A) de centre A passant par D (et F)
La perpendiculaire en A à BC coupe ce cercle en U' du côté de BC et en U" de l'autre côté.
Soit P' le symétrique de A par rapport à U'
Soit U l'autre intersection de EU' avec le cercle (A)
Les droites AU et EP' se coupent en P, centre du cercle de Soddy extérieur.
U est le point de contact de (A) avec ce cercle, et donc le cercle de Soddy extérieur est le cercle de centre P passant par U.
On opère de même avec U", P" pour construire le point de Soddy intérieur.
Cette construction devenant ici imprécise, on préfèrera la variante suivante :
On considére aussi le point V", image du point de contact avec (B) dans l'inversion de pôle F :
La perpendiculaire en B à AC coupe le cercle (B) en V", opposé à AC.
Soit Q" le symétrique de B par rapport à V"
Soit P" le symétrique de A par rapport à U" comme ci-dessus,
Le centre S du cercle de Soddy intérieur est l'intersection de EP" avec FQ".
Le point de contact U" est ramené en U, autre intersection de EU" avec (A)
(pas tracé sur la figure)
Et finalement le cercle de Soddy intérieur est le cercle de centre S passant par U
Points d'isopérimétrie et d'égal détour
Soit un triangle ABC. Trouver un point P tel que les triangles PAB, PBC, PAC aient même périmètre.
Soit le cercle (P), de centre P, tangent aux trois cercles (A) (B) (C), cercle de Soddy extérieur, qui si les cercles
(A) (B) (C) ne sont pas trop différents, entoure ces cercles.
Les cercles (A) (B) (C) étant tangents intérieurement en U, V et W.
On a : PU = PV = PW = RP rayon du cercle de Soddy
CW = CE et BV = BE
Le périmètre de PCB est donc PV + PW = 2RP
Et de même pour les deux autres triangles
Théorème : Le point de Soddy extérieur est le point d'isopérimètres
Ceci bien entendu si le cercle de Soddy externe (P) contient les cercles (A) (B) (C).
Si le plus petit des cercles (A) (B) (C) est si petit que (A) (B) (C) sont extérieurs à (P),
il n'y a pas de point d'isopérimètres.
La valeur limite est quand le cercle de Soddy externe est une droite :
UV² = AB² - (BU-AV)² = (rA + rB)² - (rA - rB)² et donc UV = 2√(rArB)
et de même pour VW et UW = UV + VW donne la condition d'existence du point d'isopérimètres :
1/√rA < 1/√rB + 1/√rC ou aussi :
| a + b + c > 4R + r
où r est le rayon du cercle inscrit et R celui du cercle circonscrit. |
Le point de Soddy intérieur est aussi le point "d'égal détour".
Appelons détour de A à B par S la quantité AS + SB - AB.
Si S est le point de Soddy intérieur, le détour est 2ρ
avec ρ le rayon du cercle de Soddy intérieur, et est le même pour AB, BC et AC.
Enfin, si le point de Soddy extérieur n'est pas le point d'isopérimètre, c'est un second point d'égal détour
(quand a + b + c < 4R + r).
De façon générale, les rayons des cercles de Soddy sont donnés par la
formule de Descartes, à partir des rayons
des cercles (A), (B), (C) qui sont
(formules classiques des points de contact du cercle inscrit)
cercle (A) : rA = AD = AE = (AB + AC - BC)/2 = p - a en appelant p le demi-périmètre de ABC
et de même pour les deux autres.
Droite de Soddy
La droite de Soddy est par définition la droite passant par les deux points de Soddy.Considérons l'inversion par le cercle inscrit à ABC, de pole I, centre du cercle inscrit et conservant les points de contact DEF inchangé
Les cercles de centres A, B, C, orthogonaux au cercle inscrit en D,E,F, sont donc globalement invariants
Cette inversion échange donc les deux cercles de Soddy.
Par conséquent les centres de ces deux cercles (les points de Soddy) sont alignés avec le pole d'inversion (centre du cercle inscrit)
| La droite de Soddy passe par le centre du cercle inscrit |
Je ne ferais pas ici les démonstrations correspondantes : elles débordent un peu du cadre "récréatif" de ce site !
Nota : le point de Gergonne est l'intersection des céviennes des points de contact du cercle inscrit
le point de Longchamps est le symétrique de l'orthocentre par rapport au centre du cercle circonscrit
Variante "exinscrite"
La condition sur le centre radical des cercles de centres A, B, C : ID = IE = IF est aussi satisfaite pour les centres des cercles exinscrits à ABC.Ce qui donne une variante avec les mêmes propriétés pour des points sans nom "ressemblant aux points de Soddy"
Pour cette variante, on trouve bien des cercles centrés en A,B,C et mutuellement tangents, mais pas extérieurement !
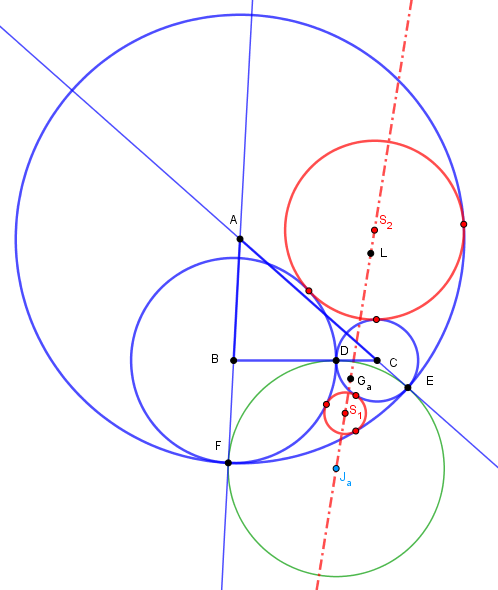
L'applet suivante montre cette variante à partir du cercle exinscrit dans l'angle A, de centre Ja et de ses points de contact que l'on continue à appeler D, E, F
L'équivalent du point de Gergonne est Ga, la droite S1S2 passe par Ja (même preuve que précédemment par l'inversion de pole Ja) et par ce point d'"ex-Gergonne" Ga, et même par le point de Longchamps L (sur la droite d'Euler OGH) de ABC !
Les 4 droites de Soddy généralisées (la droite de Soddy et les 3 droites obtenues par les cercles exinscrits) passent donc toutes par ce point de Longchamps, qui exhibe ainsi une propriété remarquable.
