Croix et étoiles
Dissections impliquant des croix et des polygones étoilés Croix grecque en carré
Croix grecque en carré
Il est immédiat de paver le plan avec une croix grecque, et de superposer un pavage avec des carrés de
côté a√5, où a est le côté de la croix (celle-ci comportant 5 petits carrés de côté a).
On peut faire varier le décalage entre les deux pavages, pour obtenir diverses dissections équivallentes, par exemple une dissection symétrique, en 4 pièces toujours.

 Croix grecque en triangle
Croix grecque en triangle
Là aussi le pavage est immédiat, mais la position à choisir pour minimiser le nombre de pièces et
ne pas avoir des pièces trop petites, ou ne tenant qu'à un fil, nécessite un peu d'astuce
(dissection de H. Lindgren).
Il est de toute façon moins immédiat de construire le côté du triangle équivallent.
L'aire de la croix est 5a² et en appelant s le côté du triangle, l'aire du triangle est (s/2)²√3.
On en tire (s/2)² = 5a²/√3 et une construction :
Reporter AS = 5 AB, et tracer la droite ST à 30°, AT = 5 AB/√3.
Le cercle de diamètre HT coupe la droite AB en P, AP² = AH.AT = (s/2)²
Construire le triangle équilatéral AMN, puis la parallèle UV à AM en N.
 Une autre dissection, plus compliquée et surtout mettant en jeu une pièce "ne tenant qu'à un fil" est
obtenue par la méthode des bandes. La bande formée par dissection de la croix est moins triviale :
Une autre dissection, plus compliquée et surtout mettant en jeu une pièce "ne tenant qu'à un fil" est
obtenue par la méthode des bandes. La bande formée par dissection de la croix est moins triviale :
La croix est coupée en deux par UV, et les deux demi croix forment une bande.
On superpose alors les deux bandes de sorte que le "point central" de la bande de croix soit au milieu M du côté AB du triangle, et que le sommet S de la croix soit sur le bord de la bande des triangles :

Ceci donne la construction de S :
L'aire de la croix est égale à celle d'un carré de côté MS
L'aire du triangle est s.h/2. Donc MS² = MM'.h/2
Reporter MH = h/2. La perpendiculaire en H et le cercle de diamètre MM' se coupent en K.
MK est le côté cherché, construire MS = MK
Construire V avec SV = MS/2 et SV_|_MS et en déduire le tracé de la croix, et la construction des découpes.
Celles-ci sont définies exclusivement par la partie commune des deux bandes. Ce qui est à l'extérieur est sans rapport.
En fait une moitié de la partie commune puisque celle-ci met en oeuvre deux croix et deux triangles.
On notera que des bandes voisines sont décalées : ceci se voit sur la dissection du triangle.
Le point important ici est la position de P par rapport au côté AB du triangle !
Il s'agit en fait de prouver que l'angle AMV est > 45°. P est donc strictement intérieur au triangle,
et les deux pièces mauves n'en font qu'une.
<)AMV = AMS + SMV = AMM' - SMM' + SMV
AMM' est bien entendu 60°
SMM' = arcsin(h/(2MS)) = arcsin( 4√3 / 2) ≈ 41.15°
enfin SMV = arctan(1/2)
On en tire AMV = 45.41°. CQFD.
Mais le fil étroit entre les deux parties de la pièce mauve rend cette dissection impraticable.
Elle a juste un intérêt théorique...
 Croix grecque en dodécagone
Croix grecque en dodécagone
Cette dissection rappelle fortement celle du dodécagone en carré, elle est basée sur le même
pavage du plan par le dodécagone (découpes en bleu).
Il reste la découpe en rouge pour obtenir une croix et non un carré.
Construisons BC = AB/2, perpendiculaire à AB. I milieu de AB.
Les triangles ABC et AUI sont semblables, le zigzag AUVB passant par I est donc la découpe cherchée (AU = UV = VB et perpendiculaires)
Les dissections de la croix grecque en d'autres polygones sont plus complexes, essentiellement à cause de
la découpe sauvage de ces polygones pour former des bandes.
On pourra s'exercer avec le pentagone, pour lequel la transformation en bande est assez simple,
de sorte que la dissection croix grecque ↔ pentagone nécessite seulement 7 pièces.
 Croix latine en triangle
Croix latine en triangle
L'aire de la croix est 6a², celle du triangle de côté s (s/2)²√3
soit (s/2)² = 2a²√3 = (2a) × (a√3) d'où la construction,
tout à fait semblable à celle de la croix grecque :
Soit A et C les milieux des grands côtés.
Une droite à 30° coupe AB en H, AH = a√3
Le cercle de diamètre AB et la perpendiculaire en H se coupent en M.
AM² = AB.AH = (2a) × (a√3) = (s/2)²
Construire le triangle équilatéral AED, puis la parallèle en D à AE.
Nota : cette parallèle passe par le sommet U.
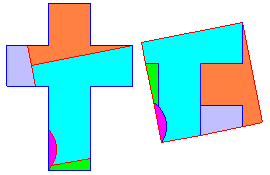 Croix latine en carré
Croix latine en carré
Une astuce déja vue ailleurs consiste ici à utiliser une pièce courbe pour éviter des pièces minuscules.
Construisons d'abord le côté du carré équivallent, de côté a√6.
 Soit AB = 5a/2. Le cercle de diamètre AB et le cercle de centre B de rayon BK = a/2 se coupent
en M et : AM² = (5a/2)² - (a/2)² = 6a²
Soit AB = 5a/2. Le cercle de diamètre AB et le cercle de centre B de rayon BK = a/2 se coupent
en M et : AM² = (5a/2)² - (a/2)² = 6a²
Complèter le carré AMNP.
Ceci conduit à une pièce minuscule JNU.
Considérons alors la rotation de centre I qui transforme CD en EF, et centre du cercle circonscrit à CNE.
Ce cercle définit ainsi une pièce plus maniable.
 Mais pourquoi faire aussi compliqué, à part le plaisir d'utiliser des découpes courbes ?
Mais pourquoi faire aussi compliqué, à part le plaisir d'utiliser des découpes courbes ?
La transformation d'une croix latine en bande de largeur 2a est immédiate, en coupant la grande branche,
et donne la dissection bien plus simple suivante :
Reportons CM = CB = a √2. Alors AM² = AC² + CM² = 4a² + 2a²
donne le côté du carré équivallent AM = a√6.
Les autres découpes à partir de la croix sont CP // AM, et KH _|_ AM passant par C.
La grande branche coupée étant placée en AEFG pour former la bande avec les croix, et on superpose cette bande avec celle formée de la répétition du carré AMUV pour définir cette dissection.
Les autres dissections impliquant les croix latines ne sont pas vraiment plus compliquées que pour la croix grecque.
Donnons la très belle dissection due toujours à H. Lindgren :
 Croix latine en dodécagone
Croix latine en dodécagone
La difficulté est ici d'imaginer le pavage avec le dodécagone. Parce que la construction est plutôt facile,
une fois ce pavage réalisé : on utilise essentiellement des diagonales du dodécagone.
On construit le triangle équilatéral, par C = BF ∩ AA'
D est obtenu de suite par I I' ∩ HH"
HE = AB sur HH' complète ainsi les découpes du dodécagone en un triangle équilatéral ABC, une pièce de forme étrange ACDEFGHI et le reliquat, ces trois pièces pavant le plan (contours magenta)
Inutile de paver effectivement le plan pour poursuivre les découpes :
L'angle K de la croix est construit par HH" ∩ B'I'
Les parallèles à AI en K et E donnent par intersections avec BB' et HH' les points N,J et R
Complèter le carré NJQP
Enfin la découpe IM est obtenue par la diagonale IB'.
Parmi les autres dissections impliquant les croix on peut citer aussi d'autres formes de croix :
svastika, croix de malte, croix "globulaire" (formée d'arcs de cercle) etc...
 Avant que la svastika prenne un aspect historique tabou, elle était assez répandue et
Sam Loyd (1841-1911 !) a proposé plusieurs problèmes et dissections avec cette croix.
En particulier une svastika "étirée" formée de 17 petits carrés sur une grille de 7×7,
et avec 17 = 4² + 1², le côté du carré équivallent est
tout trouvé !
Avant que la svastika prenne un aspect historique tabou, elle était assez répandue et
Sam Loyd (1841-1911 !) a proposé plusieurs problèmes et dissections avec cette croix.
En particulier une svastika "étirée" formée de 17 petits carrés sur une grille de 7×7,
et avec 17 = 4² + 1², le côté du carré équivallent est
tout trouvé !
La variante plus compacte sur une grille de 5×5 (10×10 carrés moitié) n'est pas plus compliquée.
Une autre croix de Sam Loyd est la "iron cross", dans sa "cyclopedia of 5000 puzzles".
En fait une large liberté est laissée à cette croix.
L'applet propose de la construire en partant du carré et du point P quelconque (draggable) dans le triangle ABC.
M est le milieu de AP, MN = MP et perpendiculaire.
NQ = BP et perpendiculaire à BP
QF // MNE (ou DF = AE)
Si P est extérieur au triangle ABC, la construction affiche n'importe quoi (aires négatives).
Si l'angle APB est obtus, ça ne ressemble même plus à une croix... plutôt à un carré muni de 4 excroissances !
En particulier si APB = 135° (P sur le cercle noir tangent à AC), BPN sont alignés on obtient alors
un carré augmenté de 4 triangles rectangles isocèles.
Le quart de cercle de diamètre AB délimite <)P = 90°, une "iron cross" n'est ainsi
obtenue que si P est au delà de ce quart de cercle.
 La croix de Malte sur un quadrillage se dissèque sans difficulté, les lignes de coupe s'appuyant
sur les points du quadrillage.
La croix de Malte sur un quadrillage se dissèque sans difficulté, les lignes de coupe s'appuyant
sur les points du quadrillage.
La croix "standard" dans un quadrillage 5×5 a pour aire 17 carrés de la grille.
Le côté c du carré équivallent est donc c² = 17u² = (4u)² + u².
c est donc la diagonale d'un rectangle de 1×4
La suite de la dissection donne des pièces de forme étrange, mais qui se déduisent naturellement
par des parallèles et les points de la grille.
La croix de Malte dans une grille de 8×8 proposée par P. Berloquin a
une aire de 40 = 6² + 2². Le côté du carré équivallent est donc la diagonale d'un rectangle de 6×2.
La dissection est nettement plus simple.
Enfin la dissection de la croix de Malte "standard" en croix grecque n'utilise que des points d'un quadrillage 4 fois plus fin (points verts), grille de 20×20, indiquée seulement 10×10 pour aérer le dessin.
 La croix potencée de 25 carrés sur une grille de 9×9 se dissèque en carré de façon évidente avec 6 pièces.
La croix potencée de 25 carrés sur une grille de 9×9 se dissèque en carré de façon évidente avec 6 pièces.
Peut on faire mieux avec des découpes en biais ? 25 = 3² + 4² ?
La croix globulaire sera vue dans les dissections courbes.
Pour en terminer avec les croix donnons la dissection (toujours de Sam Loyd) d'une croix grecque
en deux croix grecques (d'aires moitié donc).
Cette dissection est présentée car elle met en évidence la relation
arctan(1) = arctan(1/2) + arctan(1/3).

Considérons la diagonale AB de la croix grecque, diagonale d'un rectangle de 1×3
La diagonale de la croix d'aire moitié est dans le rapport √2, c'est à dire le côté d'un
triangle rectangle isocèle ABC (angle de 45°)
dont l'hypothénuse est la diagonale de départ AB.
La relation citée ci dessus prouve ainsi que cette diagonale de la croix d'aire moitié est la diagonale BC
d'un rectangle de 1×2,
donc se place idéalement en MN, M et N étant les milieux des côtés de la croix de départ.
Ainsi les sommets de la croix moitié sont aux milieux M, N, K, Q des côtés de la croix de départ.
On reconstitue alors la croix d'aire moitié à partir de MK, par une construction déja vue
lors de la dissection croix grecque ↔ dodécagone :
TK perpendiculaire à MK et égal à MK/2 donne la direction de MP.
La perpendiculaire en N à MT donne P et le reste de la croix s'en déduit.
Nota : NP passe par I, milieu de MK.
Passons maintenant au polygones étoilés. L'hexagramme est plus simple que le pentagramme, car il est facile de le transformer en bande.
 Hexagramme en carré
Hexagramme en carré
En coupant les pointes BC et EF, et en les plaçant dans un des creux en J, on obtient une bande.
L'aire de l'hexagramme est alors évidemment h×AD
Reportons AH = h. Le cercle de diamètre AD coupe la perpendiculaire en H au point K et AK² = AH.AD. AK est donc le côté du carré équivallent.
La preuve que DM = AK est aussi égal au côté du carré est immédiate en considérant les triangles égaux AHK et DIM (rectangle, angle égal A = D, et AH = DI)
Nota : M n'est PAS le milieu de EF.
en effet IM² = DM² - ID² = h.AD - h² = h²√3 - h²
et (AD/2)² = (h√3/2)² = 3h²/4, donc IM ≠ AD/2
(à 1.2 % près !)
 Hexagramme en triangle
Hexagramme en triangle
Pas besoin même de former ici une bande : l'aire de l'hexagramme est h²√3,
le côté s du triangle équivallent est donné par (s/2)²√3 donc h = s/2
Le triangle équivallent est immédiatement construit, et la dissection suit dans la foulée.
 Pentagramme en carré
Pentagramme en carré
Nous allons construire cette dissection d'après ses propriétés.
La transformation en bande du pentagramme est trop "bizarre".
La découpe de la pièce orange est sans commentaire.
L'examen des pièces rouge et jaune conduit, compte tenu des angles en O, à une pièce rouge triangle isocèle et
une découpe de ces pièces parallèlement aux côtés du pentagramme.
Les points M,N,Q,F servent de pivots pour les pièces et donc HM et KQ sont égaux à la moitié du côté a du carré.
De plus M et N sont les milieux des segments.
Enfin NH + NK = a ainsi que FH + FK = a itou, 2NF = 2a.
Donc NF = a
On pourrait certes construire le côté a du carré équivallent, et la droite NF s'en déduisant immédiatement. Nous allons toutefois construire directement H,K,F,Q à partir de la propriéte précédente, sans construire a au préalable.
 Occupons nous déja des pièces rouge et jaune et du point N.
Occupons nous déja des pièces rouge et jaune et du point N.
On a immédiatement ZR // BD et AR = ZR = ZY.
AR (pièce jaune) vient en SZ (pièce mauve) et ZR (pièces jaune + rouge)
vient en UZ (pièce mauve), soit finalement les constructions de ZS = ZU = ZY
et UV // ST // AC.
Examinons maintenant la construction de H à partir de M et N.
Angle H = 90°, H est donc sur le cercle de diamètre MN.
Il s'agit de trouver H pour que NF = 2MH.
Le milieu P de NF est donc sur la droite parallèle à CE, homothétique de CE de centre N et de rapport 1/2.
De plus NP = MH, donc NP se déduit de MH par une rotaion de 90° qui transforme M en N.
Cette rotation a ainsi pour centre le sommet I du triangle rectangle isocèle MIN,
c'est à dire le milieu de l'arc MN, intersection du cercle de diamètre MN et de la médiatrice de MN.
Le lieu de H est transformé par cette rotation en un cercle, lieu de P.
P est ainsi déterminé par l'intersection de la droite et du cercle lieux de P.
On en déduit la droite NF, puis H, puis Q (parallèle à NF à distance = MH) et donc K.
Remarque : P est le milieu de HK.
Les autres dissections de polygones étoilés entre eux ou en polygones convexes sont
généralement compliquées.
Donnons seulement :
 Hexagramme en dodécagramme
Hexagramme en dodécagramme
Due à Greg N. Frederickson.
Reporter OH = OA, puis D comme intersection de OB et AH.
Ceci donne le point de départ de la construction du petit hexagramme EDF etc. que l'on découpe en trois pièces identiques.
La construction de D assure que DB = DE, et ainsi donne le côté du dodécagone étoilé.
La parallèle à OI en M coupe IJ en N, NP est parallèle à IU.
De même pour N' et K.
Tous les petits segments ainsi construits sont égaux, et les angles ont la valeur correcte pour composer le dodécagone étoilé.
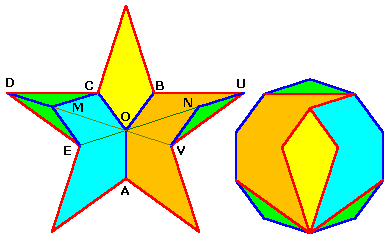 Pentagramme en décagone
Pentagramme en décagone
Les relations d'angles conduisent, comme pour l'hexagramme en triangle, à une construction simple (H. Lindgren).
Soit O le centre du pentagramme (intersection de DV et EU.
CM // EU, VN // OB.
Terminons avec les polygones étoilés par une multiplication miraculeuse :
 Octogone étoilé en 5 octogones étoilés
Octogone étoilé en 5 octogones étoilés
L'octogone étoilé est formé de la superposition à 45° de deux carrés.
En faisant abstraction des pointes, on "voit" la découpe d'un carré en 5 carrés, et √5 = √1² + 2²
Le carré ABCD est disséqué en 5 carrés par les droites joignant un sommet (A) à un milieu (M). et idem B au milieu de CD → B'C', C au milieu de AD → C'D' et finalement D au milieu de AB → A'D'.
L'octogone étoilé central est complèté par le même procédé à partir des autres sommets de l'octogone (EH etc.)
Les autres découpes se déduisent de prolongements et de parallèles aux côtés de l'octogone central : PF // EH → P et de même pour N et J.
Finalement on complète les deux petits carrés vert et cyan.
Cette construction est répétée 3 autres fois à partir des autres sommets et conduit à 4 jeux de pièces identiques donnant 4 octogones étoilés. Un seul est représenté. Le 5ème étant bien évidemment l'octogone central bleu.











