Comme un Sangaku

En prenant comme unité le rayon des petits cercles, quel est le rayon des autres ?

Appelons R le rayon AO, r le rayon CE.
OB = OE = 2R, OC = 2R - r, AC = R + r et donc dans le triangle OAC (R + r)² = R² + (2R - r)² qui se simplifie en

r = 2R/3

Soit maintenant le cercle de centre F (à définir) de rayon ρ = r/2 = R/3 et tangent aux cercles (A) et (C). Soit R = 3ρ et r = 2ρ, par conséquent OA = 3ρ, OC = 4ρ, AC = 5ρ et OB = 6ρ
CF = r + ρ = 3ρ = OA, AF = R + ρ = 4ρ = OC
Donc OAFC est un rectangle et OF = AC = 5ρ
Soit T le point opposé du cercle (F) sur le diamètre OF
OT = 5ρ + ρ = 6ρ
Le cercle (F) est donc tangent au cercle (O) en T, et est le plus petit des cercles donnés.

ρ = 1, r = 2, R = 3 et OB = 6

On a ainsi la constructionn de cette figure remarquable à partir du triangle de Pythagore (3, 4, 5), et tous les cercles de rayons entiers, sans avoir besoin d'utiliser la construction générale avec les complications des cercles inscrits dans un Arbelos (ici les demi-cercles de l'arbelos, de centres A et A' sont égaux)

On peut se poser la question générale des cercles inscrits de ce genre (4 cercles mutuellement tangents, à la Soddy), (O) (A) (C) (F), de rayons entiers, tout au moins rationnels.

Les rayons de 4 cercles mutuellement tangents sont reliés par la relation de Soddy-Descartes

2(1/a² + 1/a² + 1/a² + 1/a²) = ( 1/a + 1/b + 1/c + 1/d)²

Un script donne, par force brute, toutes les valeurs entières avec 1 ≤ a ≤ b ≤ c ≤ 20, et d rationnel (entier). de la table suivante.
Un rayon d <0 indique un cercle entourant les 3 autres,
Un cercle de rayon d infini est une droite !

La 1ère valeur (1, 2, 3, -6) est notre figure
La valeur suivante (1, 2, 3, 6/23) donne le rayon d'un cercle inscrit dans la lacune entre les cercles (C), (F) et (A), de rayons 1, 2, 3.
Ce cercle est donc aussi à rayon rationnel !
De même le cas (2, 3, 3, 2/5) donne le cercle dans la lacune entre (A) (A') (C)
Ce cercle est le cercle suivant de la chaine "à la Pappus" initiée par les cercles (A) (A') (C) de la figure.
On peut se poser la question si tous les cercles de cette chaine sont dans ce cas à rayons rationnels.
Le cercle suivant est donc le cercle intérieur de Soddy dans (3, 3, 2/5), c'est à dire le 1/5 du cercle dans (15, 15, 2) dont le tableau précédent donne la valeur 6/7, et donc finalement la valeur 6/35 avec l'échelle ρ = 1
Mais cette confirmation nécessite non pas une succession d'exemples mais une démonstration (que tous les cercles de la chaîne de Pappus sous le cercle inscrit (C) sont à rayons rationnels)

On peut se poser la même question pour la chaine de Pappus proprement dite, partant vers les côtés.
C'est à dire le suivant est dans les cercles (1, 3, -6) qui n'apparaît pas dans le tableau précédent. à part le (1, 2, 3, -6) qui est le cercle (C) et pas celui considéré.
En fait le calcul (script) avec la formule de Descartes et les rayons 1, 3, -6 donne, outre le rayon 2, le 4ème cercle pour rayon 6/11, donc rationnel
On verrait figurer ce cercle dans le tableau si on avait mis la limite à 50 au lieu de 20, sous la forme entière (6, 11, 33, -66)
Là aussi la conjecture que tous les cercles de la chaine de Pappus correspondante ont des rayons rationnels est à démontrer.
Voire même que tous les cercles de la "baderne d'Apollonius" initiée par les cercles (O) (A), (A') sont à rayons rationnels...

En tout cas, en sautant ces démonstrations, le n^ème cercle de la chaine de Pappus "latérale" (celle qui commence avec les cercles (C)=2, (F)=1, 6/11, etc) est donné par :

rn = 6/(n² + 2)

en prenant comme unité ρ = le rayon de 2ème cercle (F) de la chaine, le 1er (C) ayant pour rayon 2.
Ce qui donne les rayons successifs :

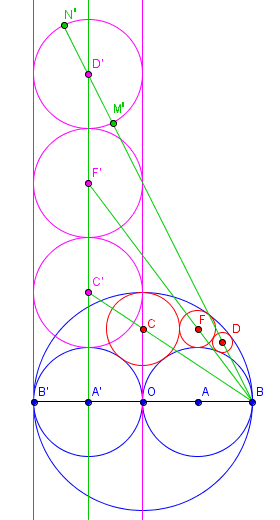Le principe de la démonstration est de considérer les relations métriques dans une inversion.
La distance M'N' entre les images par inversion de pole O et de puissance k² des points M et N est

M'N' = MN. k²/(OM.ON)

On considère alors une inversion de pole B qui conserve le cercle (A')
Cette inversion, de puissance BO.BB', échange les points O et B' et transforme :
- Le cercle (O) en la perpendiculaire en O à BB'
- Le cercle (A) en la perpendiculaire en B' à BB'
- Les cercles de la chaine de Pappus en un empilement de cercles égaux entre ces deux droites parallèles

En appelant R le rayon du cercle (A) (on a R = 3)
Le diamètre du n^ème cercle de centre D est alors
2r_n = M'N' × BO.BB'/(BM'.BN') = 2R × 8R²/(BD' - R)(BD' + R)
Avec BD'² = BA'² + A'D'² = (3R)² + (2nR)² et donc (BD' - R)(BD' + R) = BD'² - R² = (8 + 4n²)R²
Ceci donne r_n = 2R/(2 + n²) et avec R = 3 la formule avancée ci dessus.

Cette démonstration peut être rendue plus générale avec un arbelos dont les cercles de base (A) et (A') sont inégaux, donnant une formule semblable, en fonction du rapport des rayons.

 
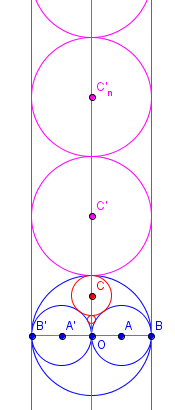Une démonstration du même genre s'applique aussi à la chaine "verticale " de cercles, transformée par une inversion judicieuse (de pôle O de puissance OB²) en un empilement de cercles égaux.
Ici c'est même encore plus simple car la distance OC'_n ne nécessite même pas le théorème de Pythagore !
On obtient la formule (avec OB = 6ρ) :

rn = 6ρ/(4n² - 1)

et les valeurs :

On retrouve bien C₁ = (C) de rayon 2, C₂ de rayon 2/5 et C₃ de rayon 6/35 déja calculés.