Autopavés (rep-tiles)
Il s'agit ici de découper une forme en morceaux superposables et semblables à la forme d'origine.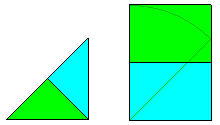
2-autopavés
Il y a un nombre fini de 2-autopavés réguliers (sans retournement des pièces) :
- Triangle rectangle isocèle
- Rectangle de rapport 1:√2 (format A4)
Les autres sont des fractales (des "fractiles") !
- Le dragon de Levy
- Le dragon de Heighway
- Les dragons jumeaux (twindragons)
- Les dragons jumeaux 'ternes' (tame twindragon)
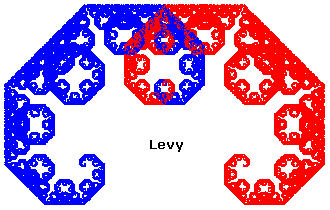
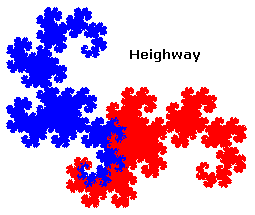
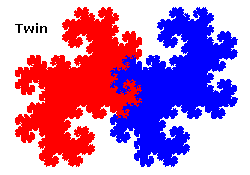
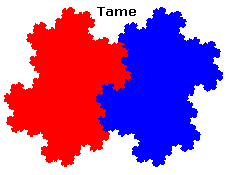
Et quelques autres aussi exotiques que le dragon de Levy, c'est à dire avec auto-intersection, pour lesquels il n'est pas évident du tout de prouver qu'il n'y a pas recouvrement, ni morceaux manquants.
Voir ici pour un bestiaire plus complet.
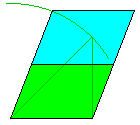
Avec retournement : le "parallélogramme A4", un parallélogramme de cotés 1:√2
3-autopavés
On a déja vu le 1/2 triangle équilatéral (équerre 30-60°) avec retournement
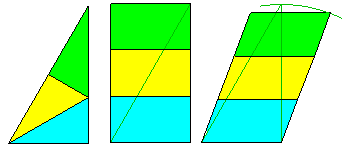
Mentionnons le rectangle de dimension 1:√3, sans retournement.
Ou avec retournement un parallélogramme dans le même rapport des côtés.
Les autres sont des fractales, par exemple :
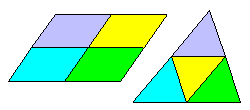4-autopavés
Il sont déja beaucoup plus nombreux.
Déja tout triangle et tout parallélogramme est de façon triviale un 4-autopavé.
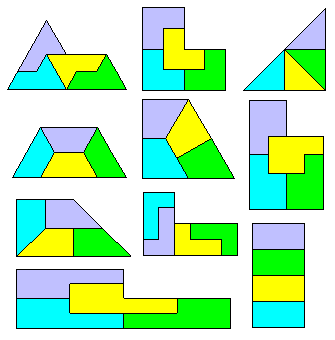Citons le tromino L, le pentomino P,
le tétromino L, le triangle rectangle isocèle (avec une découpe différente d'un triangle quelconque),
le "sphinx", divers trapèzes.
Le triomino L peut être "étiré" pour donner une famille infinie de 4-autopavés (avec retournement).
Le rectangle 1×2 permet un pavage différent du parallélogramme général.
Si on passe aux ∞-gones, la spirale triangulaire est un 4-autopavé
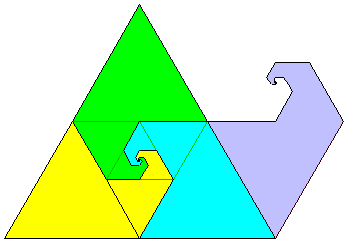
L'étape suivante est les 4-autopavés réguliers fractal ...
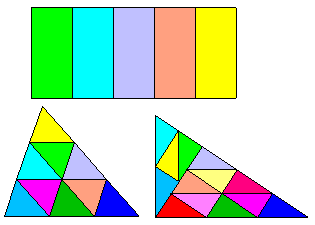Et plus
En dehors de cas très particuliers, on a déja les familles d'autopavés suivantes :
- Tout rectangle de dimension 1:√n est un n-autopavé
(avec retournement, un parallélogramme de mêmes rapports) - Tout triangle est un n²-autopavé,
- Tout triangle rectangle de côtés a, b est un (a² + b²)-autopavé, a et b entiers.
Les triangles de Pythagore sont ainsi des c²-autopavés de deux façons différentes. - Enfin tout n-autopavé est bien entendu un n²-autopavé !
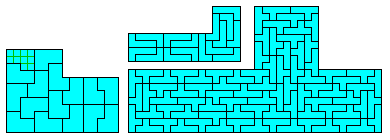On trouve aussi de nombreux autopavés à base de polyominos.
Les seuls pentominos qui soient des autopavés réguliers sont le P (déja vu) le L et le Y
Le L est "seulement" un 16-autopavé (et aussi n²-autopavés pour n>4)
Le Y est encore "pire" car c'est un 81-autopavé !
D'autres polyominos sont moins gourmands, ainsi ce 10-omino qui est un 16-autopavé.
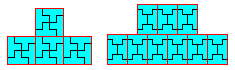Ou le tétromino L déja vu, 4-autopavé.
Parmi les tétrominos seul le T est aussi un 16-autopavé "évident".
Le même principe donne cet hexomino comme 36-autopavé.
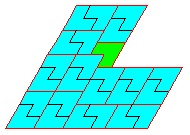Parmi les "polyamants" (sur une "grille" de triangles équilatéraux),
après le sphinx, qui est aussi un n²-autopavé pour tout n,
on considère le "homard", qui est un n²-autopavé pour n = 6k, 6k±1, ici 5²-autopavé,
ainsi que la "chauve souris" (120° au lieu de 60 du homard).
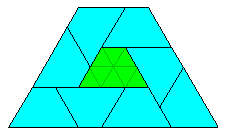
Enfin cet "octiamant" trapézoïdal est un (2n+1)²-autopavé
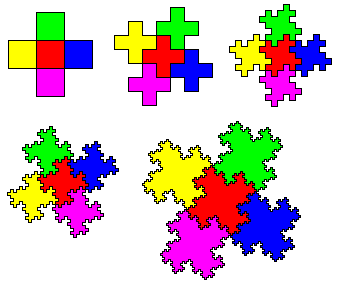On peut réaliser des n-autopavés fractal à partir d'un assemblage de polygones.
par exemple à partir de 5 carrés, on réalise un 5-autopavé fractal.
On peut faire de même avec 7 hexagones conduisant à un 7-autopavé fractal.
Sans aller si loin, en partant du 2-autopavé A4, on en déduit par ce procédé ... les dragons jumeaux !
Autopavés irréguliers
Lorsque les formes sont toutes semblables, mais de taille inégale, les autopavés sont dits irréguliers (irrep-tile)
On ne s'intéresse pas bien sûr à l'autopavage "trivial" consistant à remplacer un composant d'un n-autopavé régulier par n copies plus petites pour obtenir un (2n-1)-autopavé irrégulier ! A ce compte là un rectange A4 est un 3-autopavé !
On s'intéresse ainsi à la valeur minimum de n.
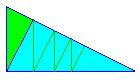Tout triangle rectangle est un 2-autopavé irrégulier, et donc par le "procédé trivial" un n-autopavé.
(on considérera avec circonspection le "∞-autopavé" en résultant, car tout pavé est un ∞-autopavé)
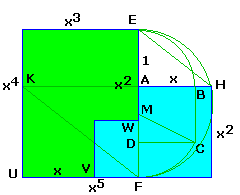Un 2-autopavé irrégulier avec x = √φ ≈ 1.272...
Voici une construction à partir d'un carré ABCD de côté 1 :
AE = AB = 1.
Le milieu M de AD donne MF = MC = √5/2 et donc AF = φ = x²
Le cercle de diamètre EF coupe AB en H, AH² = AE.AF = φ et donc AH = x.
La parallèle FK à EH donne les triangles semblables AEH et AFK, donc AK/AF = AH/AE et AK = x³,
permettant de complèter la forme extérieure.
Les découpes sont construites à partir de UV = AH = x et EW = AF = x²
Il semble que ce soit les seuls 2-autopavés irréguliers non fractals.
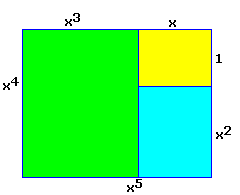
L'autopavé précédent conduit au rectangle 3-autopavé :
Un 3-autopavé pas trop dur à trouver :
L'applet permet, pour une valeur de AB/AD choisie, de chercher manuellement le point D' qui convient.
Quoi qu'il en soit C est déterminé à partir de D' par AC_|_BD'
(à cause des triangles semblables et des angles inscrits,
c'est la condition nécessaire pour que ABCD soit semblable à A'BAD')
Les quadrilatères semblables à ABCD sont alors successivement construits dans l'angle des droites AD et BC.
(DE1 // AC, E1E2 // BD, E2E3 // AC etc...)
La position de D' est à règler pour que le côté EiFi du dernier quadrilatère coïncide avec A'D'.
Les boutons "3" et "5" ramènent à des positions prédéfinies de 3-autopavés et 5-autopavés.
Le traitement des déplacements dans l'applet nécessite de répéter l'action (déplace A puis déplace D') si A a été déplacé.
Bien entendu on pourrait poursuivre et ainsi construire n'importe quel (2n+1)-autopavé de cette sorte.
Les points verts définisent le cercle de base et agissent comme zoom et déplacement de la figure.
A et D' sont déplaçables et modifient la forme du quadrilatère.
Au delà, les n-autopavés sont plus nombreux.
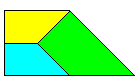
Un rectangle de dimensions 1: x avec x = √(1 + √2) ≈ 1.55377 est un 4-autopavé irrégulier
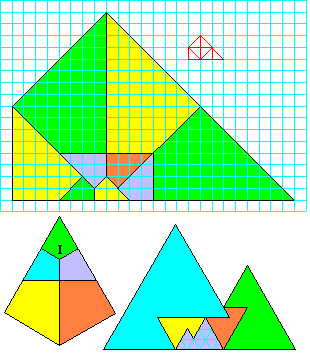Des pavages plus exotiques :
La forme composée de 7 triangles rectangle isocèles permet de construire aisément un autopavage sur
un quadrillage.
Le diamant est construit facilement en remarquant que les angles en I sont égaux, donc 120°.
Les montagnes sont de construction évidente sur une grille de triangles équilatéraux.
De très nombreux autopavés irréguliers sont des trapèzes, diverses familles infinies apparaîssent.
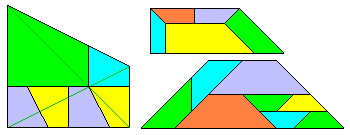
Donnons une famille de trapèzes, là aussi sous forme d'applet à "ajuster" manuellement.
Le point bleu déplaçable choisit l'angle du trapèze, les boutons 75° etc. le positionnent exactement.
La position 90° donne bien entendu des rectangles !
Les boutons numérotés choisissent l'ordre de l'autopavé de 4 à 7-autopavé.
Le procédé pouvant s'étendre aussi loin que l'on veut.
B joue le rôle de zoom, C choisit la forme du trapèze.
En déplaçant C, on ajuste les deux trapèzes cyan et verts dans le rectangle restant.
Ce réglage étant extrèmement délicat, la glissière de droite effectue un règlage fin de BC/AB.
L'erreur de remplissage du rectangle par les deux trapèzes est affichée en °/oo
Le procédé peut se généraliser à des remplissage différents du rectangle restant par 2n trapèzes.
Les autopavés irréguliers fractals existent aussi.
Quelques références:
Paver des pavés par J.P Delahaye
En anglais :
Rep-tiles introduction by S. Dutch
IFS fractal rep-tiles
Polyominoes recreational mathematics archive
mathmagic E. Friedman's Problem of the month oct/2002
