Pavages - suite

Pavages avec des pentagones irréguliers. Suite des pavages N° 10-15

E = π/2, A + D = π, 2B - D = π, 2C + D = 2π, a = e = b + d
A = π/2, C + E = π, 2B + C = 2π, d = e = 2a + c →
A = π/2, C + E = π, 2B + C = 2π, 2a = c + e = d →
A = C = π/2, 2B = 2E = 2π - D, c = d, 2c = e →
D = π/2, 2E + A = 2π, C + A = π, 2a = 2d = b = c →
D = 150°, B = 60°, C = 135°, (D = 105°), E = 90°, a = c = e, b = 2a →

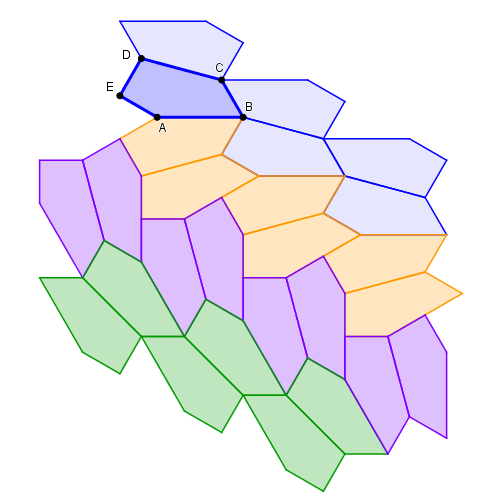
Forme 10

E = π/2, A + D = π, 2B - D = π, 2C + D = 2π, a = e = b + d
Les deux premières conditions angulaires imposent AB _|_ CD
2C + D = 2π donne BC parallèle à la bissectrice de l'angle D
La dernière condition angulaire 2B - D = π est alors redondante.

Choisissons AED avec E = π/2 et a = e.
Choisissons une direction de AB, par un point I sur le cercle de diamètre AD.
C'est à dire que la droite CD est la droite DI.
Ceci donne la bissectrice de l'angle D, et donc la direction de CD.
Il s'agit maintenant de trouver le point B tel que AB + CD = AE, CD de direction donnée.
Soit J l'intersection de la bissectrice de l'angle D avec AI.
IC = ID - CD, IB = IA - AB, donc IB + IC = IA + ID - AE
Construisons le point M avec IM = ID + IA - AE :
IA' = IA (rotation de 90°, angle droit en I), DE' = DE = AE (symétrie % DJ) donne IM = A'E'

BC // JD donne IC/ID = IB/IJ
IB + IC = IA + ID - AE s'écrit alors IB(1 + ID/IJ) = IM ou encore IB/IJ = IM/(ID + IJ)
Construisons N avec IN = ID+IJ :
IJ' = IJ (rotation de 90°) donne IN = J'D
Alors IB/IJ = IM/IN et B est obtenu comme intersection de IA avec la parallèle à JN en M.
C est obtenu immédiatement avec BC // DJ

Les limites sont définies par AB ou CD = 0.
AB = 0 et CD = DE donne alors AC = BC perpendiculaire à CE, donc C sur le cercle de diamètre AE.
CD est tangente en C à ce cercle, et donc la bissectrice de l'angle D passe par le milieu de AE.
L'angle D est alors 2 arctan(1/2) ≈ 53°

CD = 0 et AB = AE donne la bissectrice de l'angle D (de IDE) passe par B (est confondue avec BC)
Soit P l'intersection de CD et AE.
Les triangles rectangles CID et BED sont semblables (angle en D égal)
donc l'angle ICD = PCA = CPE et le triangle PAC est isocèle,
AP = AC et donc l'angle PDE = arctan (2) donne l'angle en D IDE = 2.arctan(2) ≈ 127°
Dans l'applet ci dessous, la forme de ABCD est contrôlée par le point cyan, intersection de la bisectrice de D avec la droite AE.

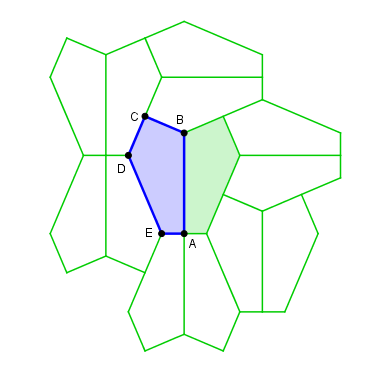
Forme 11

A = π/2, C + E = π, 2B + C = 2π, d = e = 2a + c
B + C/2 = π c'est à dire la bissectrice de l'angle C est parallèle à AB
C + E = π ou en d'autres termes D + E/2 = π (A + B + C + D + E = 3π et A = π/2)
La bissectrice de l'angle E est parallèle à CD

Choisisons C,D,E avec CD = DE.
La bisectrice de E est alors déterminée comme // CD, donc les directions de EA, AB et BC.
Reste à satisfaire CD = 2.AE + BC
Considérons une droite Ei à 60° de EA. La droite AB coupe cette droite en P et EP = 2EA
On est donc amené comme précédemment à déterminer BP de direction donnée avec CB + EP = d donné.
Les droites BC et Ei se coupent en I.
La perpendiculaire à AE en E coupe BC en J. Comme précédemment :
IP/IE = (IC + IE - d)/(IE + IJ), on construit alors IM = IE + IJ et IN = IC + IE - CD
Soit IP/IE = IN/IM et la construction de P, donc de la droite AB de A et B.

L'applet ne gère pas les conditions aux limites (a = 0 ou c = 0) autrement qu'en n'affichant rien.

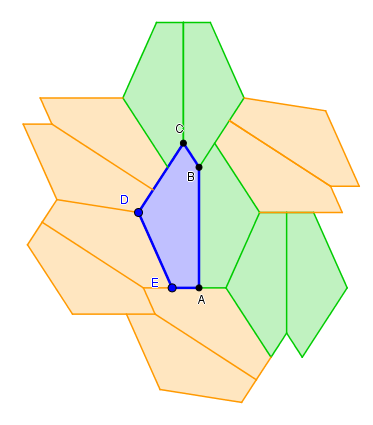
Forme 12

A = π/2, C + E = π, 2B + C = 2π, 2a = c + e = d
Choisissons C et D et les directions perpendiculaires de AB et AE : Dx et Cy
La droite BC est symétrique de CD par rapport à Cy (B + C/2 = π)
La droite DE est symétrique de Dx par rapport à CD (issue de C + E = π etc.)
Soit M avec DM = CD/2, A est sur la parallèle à DE en M.
L'ensemble de points A construits à partir de points courants B et E avec BC + DE = CD est une droite, que l'on construit par deux de ses points particuliers.
BC = 0 alors E est en E' avec DE' = CD, donnant le point A en D'
DE = 0 alors B est en C' avec C'C = CD, donnant A en C'
Le lieu de A est alors la droite C'D' et le point A est l'intersection de la parallèle à DE en M et de C'D'

Forme 13

A = C = π/2, 2B = 2E = 2π - D, c = d, 2c = e
2E = 2π - D s'écrit E + D/2 = π, c'est à dire comme précédemment AE parallèle à la bissectrice de l'angle D.
A = C = π/2 implique alors la relation B = E (puisque A + B + C + D + E = 3π)
Choisissant alors CDE quelconques avec DE = 2 CD, on en déduit B, puis la bissectrice Dj, direction de AE donc la direction de AB et donc A.

Forme 14

D = π/2, 2E + A = 2π, C + A = π, 2a = 2d = b = c
Ce pavage a été découvert en 1985 seulement par Rolf Stein.
E + A/2 = π donne DE parallèle à la bissectrice de l'angle A
A + C = π et D = π/2 donnent AB parallèle à la bissectrice de l'angle C (B + C/2 = π)

Soit A = 2t. Si on projette le tout sur la droite CD, en choisissant l'origine en C, on obtient :
2a.cos(π-2t) + 2a.cos(π/2 - t) + a. sin(t) = a et donc l'équation en sin(t) :
4.sin²(t) + 3.sin(t) - 3 = 0 soit sin(t) = (-3 + √57)/8 ≈ 0.5687293 (l'autre < -1) et donc A = 2t ≈ 69°
La solution est donc unique, à une homothétie près.
Bof.. construire √57 et dérivés...
Une remarque : 57 = 3×19 et 19 = 4² + 3 conduit à la construction suivante :

Sur deux droites perpendiculaires en O, construire avec a comme unité les points a, 2a, 3a, 4a
Puis le point OU = 3a/4, par la parallèle en (0,a) à la droite (0,4a) - (3a,0)
Reporter OV = - OU. On a alors VO = 3a/4 et VT = (3a/4) + 4a = 19a/4
Tracer le cercle de diamètre VT, il coupe la perpendiculaire en O au point N et VN² = VO.VT = (3a/4)(19a/4) = 57a²/16 soit VN = a(√57)/4
Reportons horizontalement NE = NV et retranchons NM = OU = 3a/4, il reste ME = a(√57 - 3)/4 = 2 a.sin(t)
On obtient alors immédiatement A par MA = EA = a, puis B avec AB = 2AM.
La droite BC est obtenue comme symétrique de l'horizontale Bx par rapport à AB (AB // bissectrice de C)
On reporte alors BC = BA, et on complète le pentagone ABCDE avec l'horizontale en C et la verticale en E, qui se coupent en D.

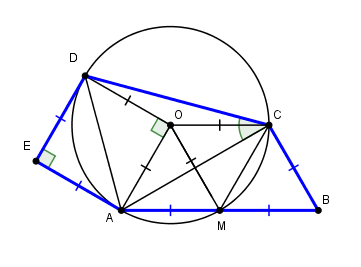
Forme 15

Ce pavage a été découvert en 2015 par ordinateur.
D = 150°, B = 60°, E = 90°, a = c = e, b = 2a
Suffisent pour définir la forme, C = 135° et D = 105° s'en déduisent, ainsi que d = (√6 + √2)/2
L'assemblage de triangles rectangles et de demi-carrés montre que les points D,A,M,C sont cocycliques
et donc ∠DCA = ∠DOA/2 = 45° et D = 3*180° - (A+B+C+E)
Pas de difficulté particulière à la construction vu les angles simples
Le pavage est un peu plus complexe :