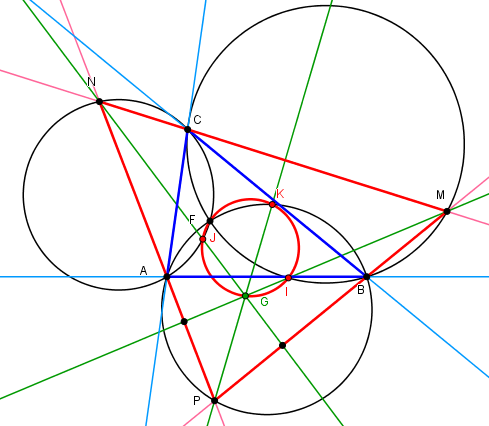
Lieux géométriques

On donne un triangle quelconque ABC
Soit MNP un triangle équilatéral circonscrit à ABC, c'est à dire avec A,B,C sur les côtés de MNP (ou prolongements).
   Lieu géométrique du centre G de MNP
Soit M'N'P' un triangle équilatéral inscrit dans ABC, c'est à dire M',N',P' sur les côtés de ABC (ou prolongements)
   Lieu géométrique du centre G' de M'N'P'
Soient M"N"P" les centres de trois cercles égaux inscrits dans ABC, (c'est à dire tangents "à l'intérieur" des droites ABC, les cercles eux même pouvant être en fait à l'extérieur)
   Lieu géométrique du centre M" d'un de ces cercles (resp. N",P")
   Lieu géométrique du centre G" de M"N"P"
(Triangle inscrit, cercles inscrits égaux)

Dans l'applet, le point M déplaçable définit les directions des triangles équilatéraux.

On peut "voir" (sans preuve) que :
Le lieu de G est un cercle, qui passe par le point de Fermat-Toricelli F de ABC.
Le lieu de G' est une ligne droite
Le lieu de M" est une hyperbole
Le lieu de G" est une hyperbole.

Bien entendu, seules des portions de ces courbes sont valides selon les conditions (sur les côtés ou leur prolongement) et les cercles à l'intérieur ou à l'extérieur.
Pour les lieux de M" et G", l'applet "saute" quand le triangle MNP est réduit au point de Fermat-Toricelli. Le cercle à considérer est le cercle de centre M1 vert et le cercle en bleu "associé". de centfe M2
Ce cercle associé est obtenu dans la construction de M" à partir de M' en choisissant l'autre côté de AB. (voir la construction générale)
Ils échangent leur rôle "brusquement" quand M vient en F, c'est à dire M' "passe" par l'infini.
L'applet génère ainsi une ligne transversale intempestive sur ces lieux.
L'autre branche de l'hyperbole est décrite quand les cercles associés bleus sont tous trois tangents "extérieurement" à ABC.

Lieu de G

Considérons les bissectrices/hauteurs/médiatrices/médianes du triangle MNP, concourantes en G, en tant que bissectrices.
GM passe par le milieu Ia de l'arc BC du cercle lieu de M.
De même GN passe par le milieu Ib de l'arc AC et GP par le milieu Ic de l'arc AB.
Le lieu de G est donc le cercle d'où on voit IaIb sous l'angle de 120°/60°
On en déduit aussi immédiatement que IaIbIc est un triangle équilatéral et que le lieu cherché est le cercle circonscrit à ce triangle.
Que le point de Fermat de ABC soit sur ce cercle est une évidence, quand le triangle MNP disparait avec M = N = P = G = F.

Cette propriété est générale pour tous les triangles circonscrits MNP de forme constante quelconque, et tout point remarquable de MNP.

Les points ABC sont draggables pour définir le triangle ABC.
La forme de MNP est définie par le point d'intersection F des cercles lieux de M,N,P, définissant ainsi les angles de ce triangle.
M est draggable sur son cercle pour faire pivoter le triangle MNP.
Un triangle arbitraire mnp est utilisé pour définir les coordonnées barycentriques de G par le point draggable g.

Lieu de G'

Ceci est une application d'un corollaire du théorème de Miquel.
Pour simplifier nous appellerons ici simplement MNP le triangle inscrit.

Théorème de Miquel :

Soient M,N,P trois points sur les côtés de ABC. Les cercles circonscrits à ANP, BMP et CMN ont un point commun S

On en déduit ultérieurement le corollaire suivant :

Tous les triangles semblables inscrits dans ABC ont le même point de Miquel S, qui est le centre de similitude de ces triangles.

Ici, tous les triangles équilatéraux MNP inscrits dans ABC ont donc le même point de Miquel S, et S est le centre de similitude de deux tels triangles.
En se plaçant dans le triangle MNP, le point S est l'unique point d'où on voit les côtés MNP sous les angles π-A, π-B, π-C.
Donc la similitude de centre S qui transforme M en N est constante. Elle transforme la droite BC en AC.
Il existe de même une similitude constante de centre S qui transforme M en P.
Tout point Q ayant des coordonnées barycentriques constantes dans MNP est ainsi obtenu à partir de M par une certaine similitude constante de centre S.
Le lieu de ce point Q est donc l'image dans cette similitude du lieu de M, c'est à dire de la droite BC, ce lieu est donc une droite.
Dans l'applet un tel point Q est déterminé par les points jaunes définissant les rapports qM/qN et QP/Qq.
En particulier le centre de gravité G de MNP, de coordonnées (1,1,1) dans MNP, parcourt une droite.
Cette droite est déterminée au plus simple en choisissant deux positions particulières de MNP.
L'applet détermine plutôt la similitude M → G ou M → Q pour tracer l'image de (BC) par cette similitude.
La forme de MNP est déterminée par le point S déplaçable, sa position en déplaçant M sur (BC)
MNP est équilatéral si S est au 1er point isodynamique X15